Get started with Octave

Download and install Octave

There are a number of Open Source alternatives to the program MatLab, one of the most known alternatives is GNU Octave. When using Octave you use a command line to enter commands. Octave can be downloaded and installed from GNU Octave.

Install on Mac

If using Mac:

Install Homebrew.

Install XCode from App Store.

Open and run the XCode app to agree to the License Agreement.

Install XQuartz.

Import science packages, open the terminal and enter:

brew tap homebrew/science

Install Octave (this takes time):

brew update && brew upgrade
brew install gcc
brew install octave --without-docs

Update:

brew update && brew upgrade

At the end of the process a summary is shown displaying the path to Octave. If following is shown:

Summary
/usr/local/Cellar/octave/3.8.1

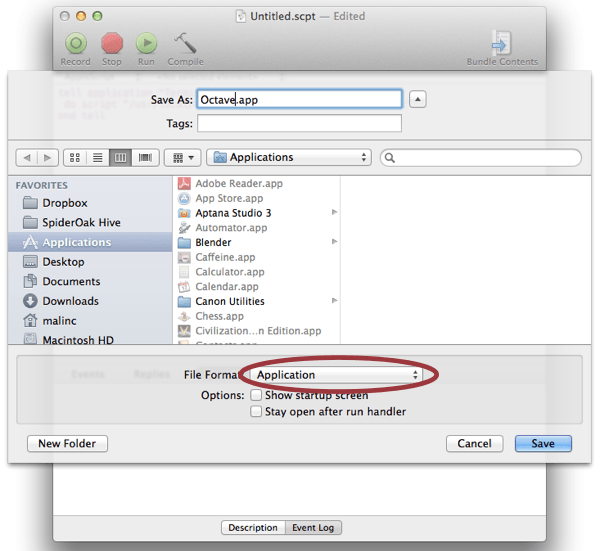
then the path to Octave is /usr/local/Cellar/octave/3.8.1/bin/Octave Open AppleScript Editor and make a New Document. Write following:

tell application "Terminal"
 do script "/path/to/octave; exit"
end tell

where /path/to/octave is the path. Save the script as Octave.app, select Application when saving.

For more information see Octave for MacOS X.

As a calculator

The easiest way to get started, is to use Octave as a calculator.

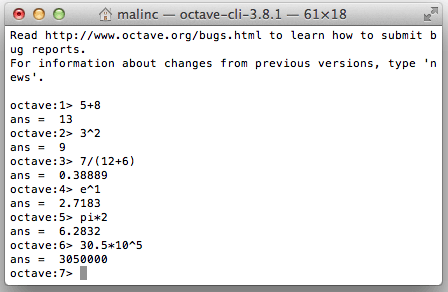
The arithmetic operators are:

There are predefined constants in Octave, some of them are listed below:

There are also a number of predefined mathematical functions in Octave, some of them are listed below:

Showing more decimals

You can show more decimals by typing format long. Go back to showing few decimals by typing format short.

Exercise 1

Calculate following expressions

1. \(\sqrt[5]{200}\)
2. \(\dfrac{3\cdot 10^{-3}}{0.001+\sqrt{0.2}}\)
    
3. \(\dfrac{2^{3+\sin{0.3}}+5}{10}\)

You should get these answers

1. ans = 2.8854
2. ans = 0.0066932
3. ans = 1.4819

You can see old commands by using up/down arrow keys.

Exercise 2

Guess the output of following commands, then check the answers given by Octave

1. 1/0 0/0 tan(pi/2)
2. inf+inf inf-inf inf/inf inf*inf
3. nan+2 nan+nan

Exit Octave

Exit Octave by writing exit or quit.

Numerical variables

When evaluating the value of an expression, the result is stored in a variable called ans (answer). You can also introduce variables of your own.

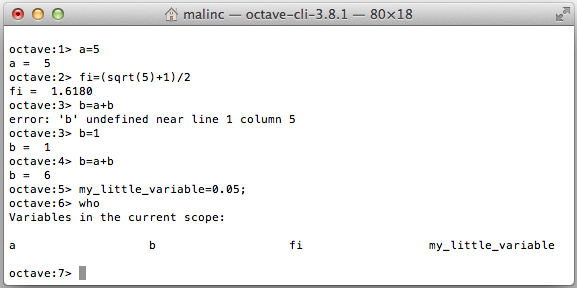
By writing who you can see all variables. If you write a semi colon at the end of the line, the output is not shown.

Naming variables

Various programs have different rules for naming entities. Although some modern programs allow for all kind of characters in names, you may run into trouble if you use characters like "-" or blank. If you want to stay on the safe side, never having to bother about naming-rules for specific programs, follow these old-school rules:

• The first character must be an english letter : a -z, A - Z
  Some programs can handle letters like å, Æ, Ç, ü; others cannot. Use english names when programming!
• The name can include numbers : 0 - 9
• The name can include underscore : _

These rules apply to Octave and a number of other programs.

Assignments

When writing a=5 at the command prompt, the equal-sign should not be thought of as a logical equality; a is not equal to 5, it is assigned the value 5. Having that in mind, one can write assignments like this

a=a+1

The statement above would be false if it was a logical statement, it is however not a logical statement but an assignment. The right-hand-side of the statement is calculated first, the result is then assigned to the variable on the left-hand-side.

Hiding the output and repeating previous commands

You can write several commands on one line by using comma, or semi colon. By using up-arrow, you can repeat the previous command, and alter it.

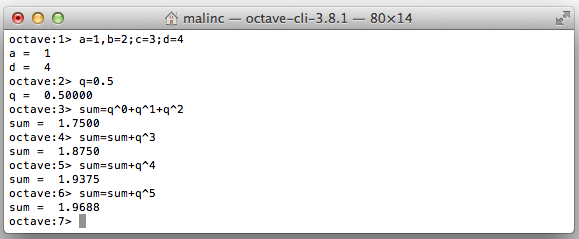
You can calculate a geometric series by using up-arrow several times.

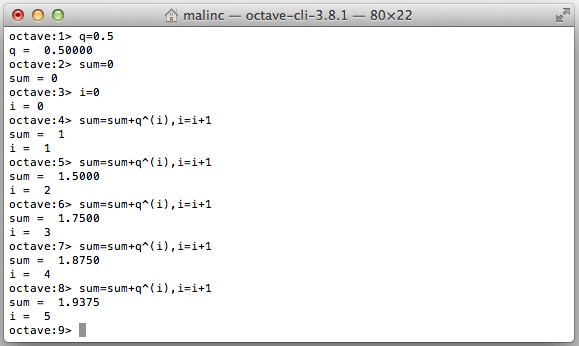
Exercise 3

Calculate the series:

(The answer is 1.5962)

Exercises on Sequences

A sequence is a function with the domain being the natural numbers. A sequence can be written like this \(a_0,a_1,a_2,...\) or like this

Recurrence equations

A geometric progression can be defined in different ways. Consider the infinite geometric progression \(3, 3\cdot 2, 3\cdot 2^2,...\).

You can describe the geometric progression in two ways.

A recurrence equation:

An explicit formula:

Exercise 4

Use Octave to find the limit as \(n\rightarrow\infty\) of following sequences. Type format long to show more decimals. Try different initial values \(c\), do you get different limits?

1. \[ \left\{ \begin{align} a_0 &=c \\ a_{n+1} &=1+\frac{1}{a_n}, n\geq0 \end{align} \right. \]
2. \[ \left\{ \begin{align} a_0 &=c \\ a_{n+1} &=\sqrt{1+a_n}, n\geq0 \end{align} \right. \]

Try to explain your answers. If you fail, do the exercises on Calculus - Fixpoints.