Kom igång med Octave

Ladda ner och installera Octave

Det finns ett antal fria alternativ till programmet MatLab, ett av de mer kända alternativen är GNU Octave. Octave används med hjälp av en kommandorad. Octave kan laddas ner och installeras från GNU Octave.

Installera på Mac

Om du använder Mac:

Installera Homebrew.

Installera XCode from App Store.

Ö֖ppna och kör XCode-appen för att gå med på lincensvillkoren.

Installera XQuartz.

Importera science-paket, öppna terminalen och skriv in:

brew tap homebrew/science

Installera Octave (detta tar tid):

brew update && brew upgrade
brew install gcc
brew install octave --without-docs

Uppdatera:

brew update && brew upgrade

Vid slutet av processen visas sökvägen till Octave. Om följande visas:

Summary
/usr/local/Cellar/octave/3.8.1

är sökvägen till Octave /usr/local/Cellar/octave/3.8.1/bin/Octave Öppna AppleScript Editor och välj New Document. Skriv in följande:

tell application "Terminal"
 do script "/path/to/octave; exit"
end tell

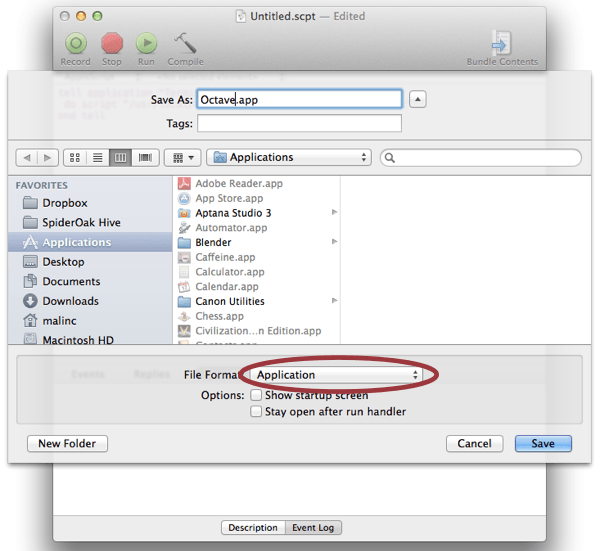
För mer information se Octave for MacOS X.

Som en miniräknare

Det enklaste sättet att börja, är att använda Octave som en miniräknare.

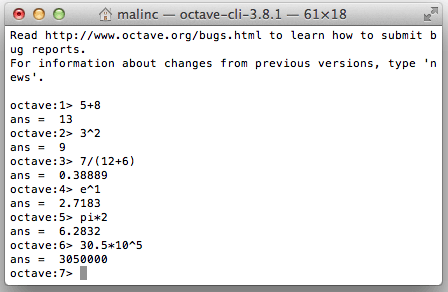
De aritmetiska operatorerna är:

Det finns fördefinierade konstanter i Octave, några av dem listas nedan:

Det finns också fördefinierade matematiska funktioner i Octave, några av dem listas nedan:

Visa fler decimaler

Man kan räkna med fler decimaler genom att skriva format long. Vill man återgå till att visa färre decimaler skriver man format short.

Övning 1

Beräkna följande uttryck:

1. \(\sqrt[5]{200}\)
2. \(\dfrac{3\cdot 10^{-3}}{0.001+\sqrt{0.2}}\)
    
3. \(\dfrac{2^{3+\sin{0.3}}+5}{10}\)

Du bör få dessa svar:

1. ans = 2.8854
2. ans = 0.0066932
3. ans = 1.4819

Du kan se gamla kommandon med upp/ner piltangent.

Övning 2

Gissa resultaten av följande uttryck, kolla svaren du får av Octave.

1. 1/0 0/0 tan(pi/2)
2. inf+inf inf-inf inf/inf inf*inf
3. nan+2 nan+nan

Avsluta Octave

Du avslutar Octave genom att skriva exit eller quit.

Numeriska variabler

Då värdet av ett uttryck beräknas, så lagras resultatet i en variabel ans (answer). Man kan också introducera egna variabler.

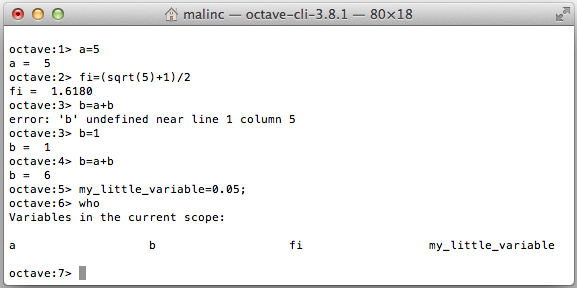
Genom att skriva who får du se alla variabler. Om du avslutar raden med ett semikolon visas inte utskriften.

Variabelnamn

Olika program har olika regler för hur man namnger saker. Även om en del moderna program tillåter många olika tecken, så kan man ibland få problem med tecken som exempelvis "-" eller blank. Om man vill vara på den säkra sidan och inte behöva bry sig om namnregler för specifika program kan man följa dessa "old-school" regler:

• Första tecknet skall vara en engelsk bokstav: a -z, A - Z
  En del program kan hantera tecken som å, Æ, Ç, ü; andra program kan det inte. Använd engelska namn då du programmerar!
• Namnet kan innehålla siffror: 0 - 9
• Namnet kan innehålla understreck: _

Dessa regler gäller Octave och ett antal andra program.

Tilldelningar

Då man skriver a=5 vid kommandoprompten, skall likhetstecknet inte tolkas som en logisk likhet; a är inte lika med 5 utan det tilldelas värdet 5. Med detta i åtanke kan man skriva

a=a+1

Raden ovan vore falsk om det var en logisk likhet, det är emellertid inte en likhet utan en tilldelning. Högersidan av tilldelningen beräknas först, resultat tilldelas sedan variabeln på vänster sida.

Göm utskriften och repetera tidigare kommandon

Du kan skriva flera kommandon på en rad genom att använda komma, eller semikolon. Med hjälp av uppåtpil, kan du repetera tidigare kommandon, och ändra dem.

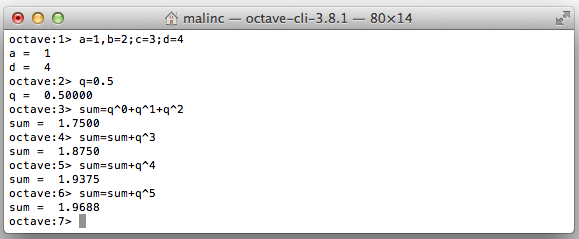
Du kan beräkna en geometrisk serie genom att använda uppåtpil upprepade gånger.

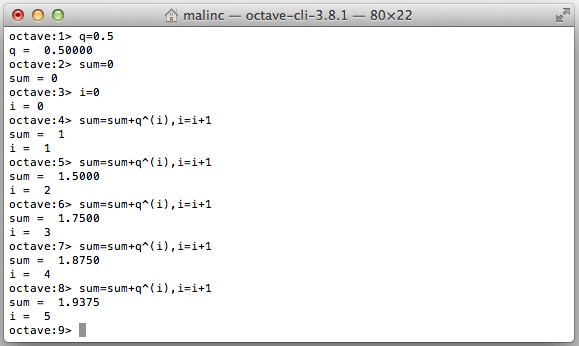
Övning 3

Beräkna serien:

(Svaret är 1.5962)

Övningar på talföljder

En talföljd är en funktion med de naturliga talen som definitionsmängd. En talföljd kan skrivas så här: \(a_0,a_1,a_2,...\) eller så här:

Rekursivt definierade talföljder

En geometrisk talföljd kan definieras på olika sätt. Betrakta den geometriska talföljden \(3, 3\cdot 2, 3\cdot 2^2,...\).

Talföljden kan definierad på två olika sätt.

En rekursiv definition:

En explicit formel:

Övning 4

Använd Octave för att beräkna gränsvärdena då \(n\rightarrow\infty\) av följande talfäljder. Skriv format long för att visa fler decimaler. Prova olika värden på \(c\), blir det olika gränsvärden?

1. \[ \left\{ \begin{align} a_0 &=c \\ a_{n+1} &=1+\frac{1}{a_n}, n\geq0 \end{align} \right. \]
2. \[ \left\{ \begin{align} a_0 &=c \\ a_{n+1} &=\sqrt{1+a_n}, n\geq0 \end{align} \right. \]

Försök förklara svaren. Om du misslyclas, gör övningarna på sidan Analys - Fixpunkter.