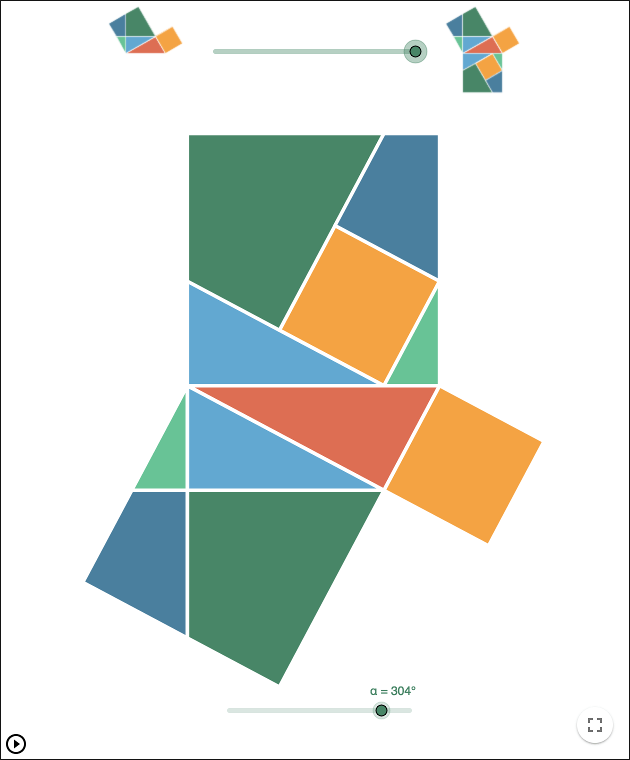Pythahoras & Thales

Pythagoras sats

Ladda GeoGebra-arbetsblad

För en rätvinklig triangel med kateterna a och b, och hypotenusan c, är

\[c^2=a^2+b^2\]

Omvänt gäller att om tre positiva tal a, b, c uppfyller likheten \(c^2=a^2+b^2\); så kan talen utgöra sidorna i en rätvinklig triangel.

Det finns en mängd bevis för Pythagoras sats som bygger på att man tolkar kvadraten av ett tal som arean av en kvadrat. Man visar sedan att de två mindre kvadraterna i bilden nedan, sammanlagt har lika stor area som den stora kvadraten.

Ett av de enklaste bevisen visas i arbetsbladet ovan. Ett något svårare bevis där de mindre kvadraterna klipps sönder och sätts ihop som en större kvadrat visas nedan.

Ladda GeoGebra-arbetsblad

Thales sats

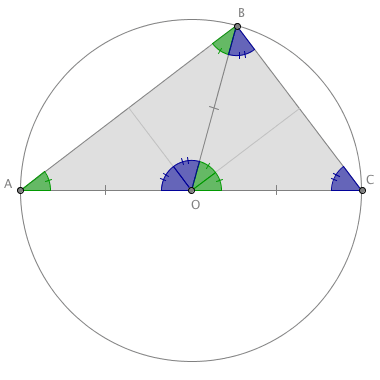
Ett enkelt sätt att konstruera en rätvinklig triangel, är att använda Thales sats. Thales sats säger att om en sida i en triangel ligger längs en cirkels diameter, och om det tredje hörnet också ligger på cirkeln, så är vinkeln vid det tredje hörnet en rät vinkel.

Övning 1

Använd bilden ovan och yttervinkelsatsen för att bevisa Thales sats!

Dynamiskt Pythagoras träd

Genom att använda Thales sats kan man göra en dynamisk version av en fraktal som kallas Pythagoras träd.

Övning 2

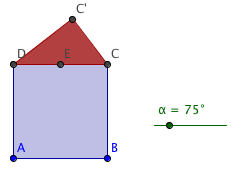
• Skapa två punkter \(A\) och \(B\) samt en glidare \(\alpha\) som representerar en vinkel. Använd verktyget Regelbunden polygon för att göra en kvadrat som i bilden ovan.
• Använd verktyget Mitt eller medelpunkt för att göra mittpunkten \(E\) mellan \(C\) och \(D\). Använd verktyget Rotera objekt kring punkt med vinkel, för att rotera \(C\) runt \(E\) med vinkeln \(\alpha\). Ändra på glidaren för att se punkten \(C'\) röra sig. Gör en triangel som i bilden ovan. Triangeln kommer tack vare Thales sats att vara en rätvinklig triangel.
• Välj Verktyg -> Skapa nytt verktyg. Gör ett verktyg som har objekten \(C\), \(C'\), \(D\), samt de två polygonerna som Färdigt objekt. Verktyget kommer att ha \(A\), \(B\), och \(\alpha\) som inmatningsobjekt.
• Bygg ett träd med hjälp av verktyget. Börja med att klicka på två punkter, skriv sedan in α in inmatningsrutan som dyker upp.

Man kan variera uppritandet av Pythagoras träd. För några exempel se Variations on Pythagoras' Tree.