Från Eratosthenes till stjärnparallax

Eratosthenes ≈ 200 f.Kr, jordens storlek

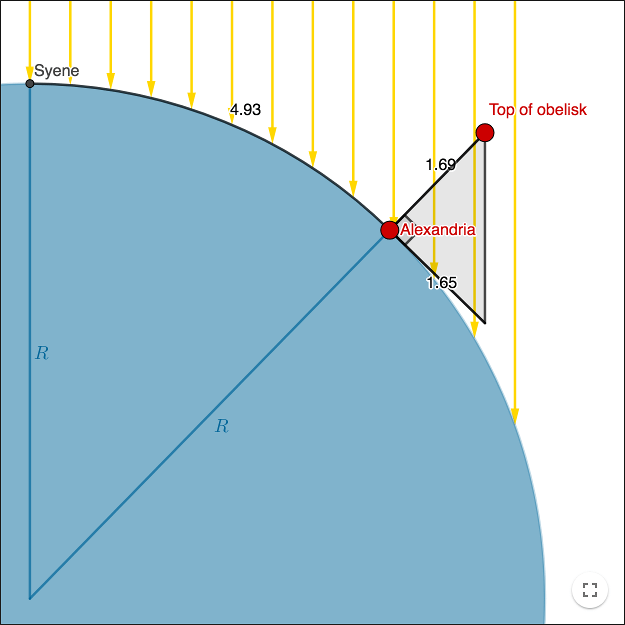
Eratosthenes var bibliotekarie vid det kungliga biblioteket i Alexandria. Han läste i en bok att när det var sommarsolstånd mitt på dagen i Syene, var allt vatten djupt ner i en brunn upplyst av solen. Han insåg att vid denna tidpunkt stod solen i zenit, den var rakt ovanför brunnen. Vid samma tidpunkt fanns det skuggor i Alexandria. Alexandria och Syene ligger på ungefär samma meridian, Alexandria är norr om Syene. Eratosthenes uppskattade avståndet mellan Syene och Alexandria. Sedan mätte han skuggan av en obelisk med känd höjd i Alexandria, vid middagstid när det var sommarsolstånd, och beräknade jordens omkrets.

Övning

Uppskatta jordens storlek med Erathostenes metod

Den enhet som används i arbetsbladet är 1000 km. Avståndet mellan Syene och Alexandria är egentligen 1000 km (dvs 1 i arbetsbladet). För enkelhetens skull antar vi att avståndet är längre och att obelisken är några tusen kilometer hög.

Om skuggan av en obelisk mäts, ligger denna egentligen på ytan av en sfär och formar egentligen inte en rätvinklig triangel som i arbetsbladet. Om bilden hade varit skalenlig, vore felet från att approximera med en rätvinklig triangel, det felet hade varit mindre än fel från andra mätningar.

Beräkna cirkelns radie i arbetsbladet (jordens radie).

Ptolemaeus ≈ 150 e.Kr, universum

Aristoteles (≈350 BC) beskrev universum som bestående av sfärer med jorden som mittpunkt. Alla objekt på himlen satt fast i en sfär och rörde sig i cirkulära banor runt jorden. Vissa observationer av himlen kunde beskrivas av denna modell men inte alla.

Ptolemaeus hittade på en annan modell där himlakropparna satt fast på, inte en sfär, utan en cirkel på sfären, en så kallad epicykel. Denna modell kunde förklara himlakropparnas observerade banor.

Genom att sätta epicykler på epicykler på epicykler...kan vilken planetbana som helst beskrivas, faktum är att vilken bana som helst kan konstrueras.

Tycho Brahe 1546-1601, planetrörelser

Tycho Brahe byggde instrument för att betrakta himlakroppar. Han kunde med sina instrument mäta vinklar med en noggrannhet som tidigare inte varit möjlig. Han byggde kvadranter och sextanter. Med dessa instrument och med hjälp av en kompass kunde han bland annat kunde mäta himlakroppars höjd över horisonten. Tycho Brahe skrev ned sina observationer och hans mätdata användes efter hans död av Johannes Kepler som med hjälp av dessa data formulerade Keplers lagar.

Kvadranter, sextanter och oktanter

En kvadrant är en fjärdedels cirkel. Med hjälp av en kvadrant kan man mäta en himlakropps höjd över horisonten. Tycho Brahe byggde en murkvadrant placerad vid muren till hans observatorium Uraniborg.

En sextant är en sjättedels cirkel. Gissa vad en oktant är!

Tycho Brahe och geocentrism

Tycho Brahe trodde bara på sådant han kunde observera. Eftersom han inte kunde observera någon stjärnparallax, drog han slutsatsen att jorden inte rörde på sig. En anledning till att han inte kunde se någon stjärnparallax skulle kunna vara att stjärnorna var för långt borta; att den vinkel de gav upphov till var mindre än de vinklar Tycho Brahe kunde mäta. Det skulle dröja ytterligare några hundra år innan en stjärnparallax kunde observeras.

Stjärnparallax

En parallax är det fenomen som uppträder då man betraktar ett objekt från två olika observationspunkter, exempelvis två ögon. Om man håller upp ett finger och betraktar det omväxlande med höger och vänster öga, så ser det ut som fingret rör sig relativt bakgrunden.

Om man vill observera en parallax då man betraktar ett objekt som är långt borta, som en stjärna, måste de två observationspunkterna vara på ett visst avstånd från varandra.

Den första stjärnparallaxen observerades 1838 av Friedrich Bessel. Han fann att stjärnan 61 Cygni hade en parallax på 0.314 bågsekunder, d.v.s. den vinkeln stjärnan har då den betraktas från jordens bana runt solen är 0.314/3600 grader.

Enheten för att mäta avståndet till stjärnor är parsek, parallaxen en bågsekund.

Hipparcos-satelliten