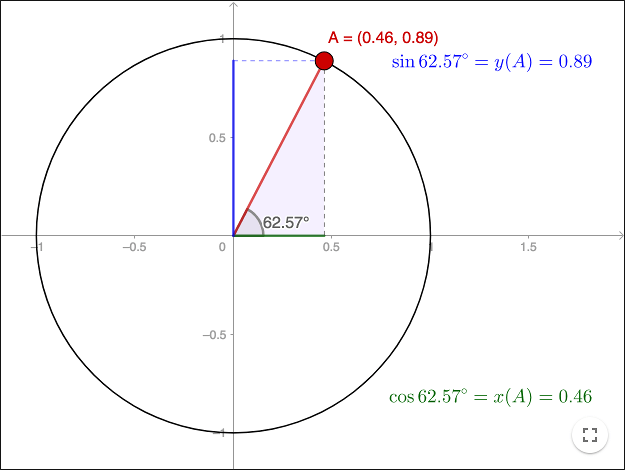
Enhetscirkeln

Eftersom the trigonometriska förhållandena inte beror på triangelns storlek, kan man alltid välja en rätvinklig triangel för vilken hypotenusan är ett. En sådan triangel kan placeras i ett koordinatsystem så att ett hörn hamnar på en cirkel med radien ett. En cirkel med radien ett kallas för en enhetscirkel. Då hypotenusan är ett, är sinus och cosinus:

\[\sin \alpha = \frac{\text{opp}}{\text{hyp}}=\text{opp} \hspace{1cm} \cos \alpha = \frac{\text{adj}}{\text{hyp}}=\text{adj}\]

Ladda GeoGebra-arbetsblad

I arbetsbladet ser man också att \(\sin \alpha = y(A)\) och \(\cos \alpha = x(A)\) där \(x(A)\) och \(y(A)\) är \(x\)- respektive \(y\)-koordinaten till \(A\). Om man använder koordinaterna till \(A\), istället för förhållanden mellan sidor i en rätvinklig triangel, kan man utvidga definitionerna av sinus och cosinus så att de är definierade för alla vinklar.

I GeoGebra, visas alla vinklar som icke-negativa och mindre än \(360^\circ\). Om en vinkel dras från positiva \(x\)-axeln i medurs riktning, är den emellertid en negativ vinkel. Dessutom kan vinklar vara större än \(360^\circ\). Om man använder enhetscirkeln för att definiera sinus och cosinus, så blir dessa funktioner definierade för alla vinklar. Observera att triangeldefinitionen fortfarande är giltig för en vinkel \(\alpha\) om \(0\lt \alpha \lt 90^\circ\).

Graferna till sinus och cosinus

Ladda GeoGebra-arbetsblad

Om man skriver sin(x) eller cos(x) i GeoGebras inmatningsrad, så plottas graferna till sinus och cosinus för alla värden på \(x\). De delar av graferna som visas i appleten ovan, upprepas oändligt många gånger. Funktionerna är periodiska med perioden \(360^\circ\).

Om \(f(x)\) är en periodisk funktion med perioden \(P\), så är \(f(x)=f(x+P)\) för alla \(x\).

Plotta trigonometriska funktioner med användning av grader i GeoGebra

Notera att skalan på \(x\)-axeln inte överensstämmer med vinkeln. Detta beror på att GeoGebra använder enheten radianer istället för grader. Om man vill att GeoGebra skall använda grader, måste man skriva tecknet för grader, tryck på Ctrl+O för att skriva tecknet för grader. Koden skall se ut så här: sin(x°) eller cos(x°).

Skala om \(x\)-axeln genom att trycka på Shift och dra sedan i \(x\)-axeln. I egenskapsfönstret för ritytan kan man ändra avståndet mellan de sträck som visas och även visa tecknet för grader som enhet.

Utvidga definitionen av tangens och cotangens

Om man använder triangeldefinitionen, så definieras tangens och cotangens så här:

Ladda GeoGebra-arbetsblad

Med hjälp av likformiga trianglar kan man visa att konstruktion i arbetsbladet stämmer för vinklar som kan användas i rätvinkliga trianglar. Nu kan vi utvidga definitionen till att gälla alla vinklar genom att istället använda koordinater av \(P\) och \(Q\), som i arbetsbladet.

Graferna till tangens och cotangens

Ladda GeoGebra-arbetsblad

Tangens och cotangens är periodiska funktioner med perioden \(180^\circ \).

\(\tan \alpha\) är inte definierad då \(\alpha = 90^\circ +n\cdot 180^\circ, n \in \mathbb{Z} \).

\(\cot \alpha \) är inte definierad då \(\alpha = n\cdot 180^\circ, n \in \mathbb{Z} \).

Radianer

Ladda GeoGebra-arbetsblad

I arbetsbladet ovan är \(x\)-koordinaterna till den blå, den gröna och den orangefärgade punkten, givna av vinkeln. Om man betraktar markeringarna längs \(x\)-axeln, ser man att ett varv inte motsvaras av 360 utan av \(2\pi\). Med andra ord motsvarar ett varv den röda punktens bana, vilken är enhetscirkelns omkrets.

Man kan ändra vinkelmått i GeoGebra under Inställningar->Inställningar..., välj sedan Avancerat-fliken.

Övningar

Övning 1

Cirkelbågar

• Gör en enhetscirkel genom två punkter \(A=(0,0)\) och \(B=(1,0)\).
• Gör en punkt \(C\) på cirkeln och markera vinkeln \(\angle BAC\).
• Se till att radianer används som vinkelmått under Avancerat-fliken under Inställningar->Inställningar....
• Använd verktyget Cirkelbåge (medelpunkt och två randpunkter) på punkterna \(A, B, C\).
• Ändra cirkelns radie och vinkeln. Observera bågens längd!

Vad är bågens längd uttryckt i radien \(r\) och vinkeln \(\alpha\) om vinkelmåttet radianer används?

Vad är längden om vinkelmåttet grader används?

Övning 2

Cirkelsektorer

• Ta bort cirkelbågen.
• Använd verktyget Cirkelsektor (medelpunkt och två randpunkter) på punkterna \(A, B, C\).
• Ändra cirkelns radie och vinkeln. Observera sektorns area!

Vad är sektorns area uttryckt i radien \(r\) och vinkeln \(\alpha\) om vinkelmåttet radianer används?

Vad är arean om vinkelmåttet grader används?