Trigonometriska identiteter
Identitet och ekvation
Skillnaden mellan likheterna \(x(x-1)=0\) och \(x(x-1)=x^2-x\), är att den första likheten är sann för vissa \(x\), medan den andra är sann för alla \(x\). En likhet som är sann för alla värden är en identitet. I vissa böcker används tecknet \(\equiv \) för att beteckna en identitet, som i \(x(x-1)\equiv x^2-x\).
Identiteter ur enhetscirkeln
Vilka av följande identiter är sanna?
| \(\sin \alpha = \sin (-\alpha)\) | \(\sin \alpha = \cos (90^\circ -\alpha)\) | \(\sin \alpha = \sin (180^\circ -\alpha)\) | \(\sin \alpha = \cos (270^\circ -\alpha)\) |
| \(\sin \alpha = -\sin (-\alpha)\) | \(\cos \alpha = \sin (90^\circ -\alpha)\) | \(\sin \alpha = -\sin (180^\circ -\alpha)\) | \(\cos \alpha = \sin (270^\circ -\alpha)\) |
| \(\cos \alpha = \cos (-\alpha)\) | \(\sin \alpha = -\cos (90^\circ -\alpha)\) | \(\cos \alpha = \cos (180^\circ -\alpha)\) | \(\sin \alpha = -\cos (270^\circ -\alpha)\) |
| \(\cos \alpha = -\cos (-\alpha)\) | \(\cos \alpha = -\sin (90^\circ -\alpha)\) | \(\cos \alpha = -\cos (180^\circ -\alpha)\) | \(\cos \alpha = -\sin (270^\circ -\alpha)\) |
Additionsformler för sinus
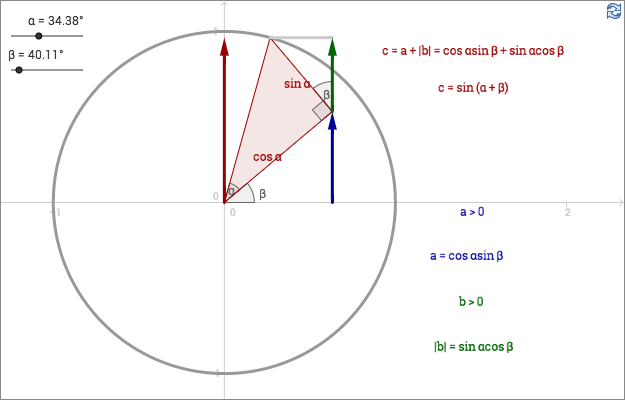
I appleten ovan är en vinkel i varje kvadrant härledd ur bilden nedan.

Dessutom används följande identiter:
\[\sin(\beta -90^\circ)=-\sin(90^\circ -\beta)=-\cos \beta \]
\[\cos(\beta-180^\circ)=\cos(180^\circ-\beta)=-\cos\beta \]
\[\sin(\beta -270^\circ)=-\sin(270^\circ -\beta)=\cos \beta \]
I denna demonstration är \(\alpha\) begränsad till \(0^\circ \lt \alpha \lt 90^\circ \) eftersom den är en vinkel i en rätvinklig triangel. Det finns inga begränsningar på \(\beta \), den kan vara i vilken kvadrant som helst. Den restriktion som syns i appleten ovan, \(0 \le \beta \lt 360^\circ \), beror på att GeoGebra bara kan visa dessa vinklar.
Genom att använda identiteterna \(\sin(-\beta)=-\sin(\beta)\) and \(\cos(-\beta)=\cos(\beta)\) får vi att:
\[\sin(\alpha-\beta)=\sin(\alpha + (-\beta))=\sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta)=\sin \alpha \cos \beta - \cos \alpha \sin \beta\]
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta + \cos \alpha \sin \beta\]
\[\sin(\alpha-\beta)=\sin \alpha \cos \beta - \cos \alpha \sin \beta\]
Additionsformler för cosinus
Utöver de identiteter som används för att förklara additionsformlerna för sinus, används även följande identiteter i appleten ovan:
\[\cos(\beta -90^\circ)=\cos(90^\circ -\beta)=\sin \beta \]
\[\sin(\beta-180^\circ)=-\sin(180^\circ-\beta)=-\sin\beta \]
\[\cos(\beta -270^\circ)=\cos(270^\circ -\beta)=-\sin \beta \]
Genom att använda identiteterna \(\sin(-\beta)=-\sin(\beta)\) och \(\cos(-\beta)=\cos(\beta)\) får vi att:
\[\cos(\alpha-\beta)=\cos(\alpha + (-\beta))=\cos \alpha \cos (-\beta) - \sin \alpha \sin (-\beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta\]
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta - \sin \alpha \sin \beta\]
\[\cos(\alpha-\beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta\]
Då bägge vinklarna är större än 90°
Additionsformlerna gäller även då bägge vinklarna är större än \(90^\circ\). Antag att \(90^\circ\lt \alpha \lt 180^\circ\). Låt \(\alpha ' =\alpha -90^\circ\). Från enhetscirkelns symmetri får vi att \(\sin \alpha =\sin(90^\circ +\alpha ')=-\cos \alpha '\) och \(\cos \alpha=\cos(90^\circ+\alpha ')=-\sin\alpha '\). Med hjälp av dessa identiteter får vi att:
\[\sin(\alpha + \beta)=\sin(90^\circ + \alpha ' + \beta)=-\cos(\alpha ' +\beta )\]
Nu kan additionsformeln användas eftersom \(\alpha ' \lt 90^\circ \).
\[-\cos(\alpha ' +\beta )=-\cos \alpha ' \cos \beta +\sin \alpha ' \sin\beta = \sin\alpha\cos\beta+\sin\beta\cos\alpha\]
På liknande sätt kan man visa att alla additionsformler gäller för alla vinklar.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License