Konstruktioner

Det som är utmärkande för dynamisk (eller interaktiv) geometri är att man ska kunna förändra ett geometriskt objekt genom att dra i punkter utan att vissa egenskaper förändras.

Om du ritar en rektangel på ett papper är detta bara ett exempel på en rektangel. Om du ritar en rektangel i GeoGebra genom att på fri hand placera fyra punkter, så kan du förstöra rektangeln genom att dra i en av punkterna.

Ska du göra en rektangel som en konstruktion, måste du tänka igenom vilka som är de utmärkande egenskaperna för en rektangel. När konstruktionen är klar ska du kunna förändra rektangeln genom att dra i vissa hörn utan att rektangelns egenskaper försvinner; konstruktionen ska klara dragningstestet.

Ladda GeoGebra-arbetsblad

Konstruera en egen rektangel! När du är klar kan du gömma linjerna. Dra i de tre rörliga punkterna. Hur du än drar i punkterna ska polygonen alltid vara en rektangel.

Fria och beroende objekt

En konstruktion innehåller alltid objekt som beror på andra objekt. Det är skillnad på fria och beroende objekt.

Prova att skapa följande objekt:

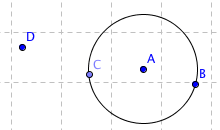
• Gör en cirkel med hjälp av punkter A och B.
• Gör en punkt C på cirkeln
• Gör en punkt D som inte ligger på cirkeln
• Flytta på punkterna

Du kan flytta punkten D fritt. Om du flyttar A eller B ändras cirkeln, dessa punkter definierar cirkeln. Punkterna A och B är fria objekt men cirkeln är ett beroende objekt, den beror på punkterna.

Om du flyttar C så rör den sig längs cirkeln. C är definierad som en punkt på cirkeln, den är därför beroende.

Betrakta algebrafönstret och välj Sortera på: Beroende; punkten C och cirkeln c visas som beroende objekt.

Skärningspunkter

En skärningspunkt är ett beroende objekt som beror på de två objekt som skär varandra. Till skillnad från en punkt på en cirkel kan en skärningspunkt inte dras runt. En skärningspunkt ritas upp som svart. Håll därför ett öga på punktens färg när du försöker skapa en skärningspunkt. Om din avsedda skärningspunkt inte är svart, har du misslyckats med att pricka skärningen mellan två objekt.

Det går oftast bra att använda verktyget Punkt för att skapa skärningspunkter. Om du emellertid vill skapa en skärningspunkt där fler än två objekt skär varandra, kan det vara enklare att använda verktyget Skärning mellan två objekt.

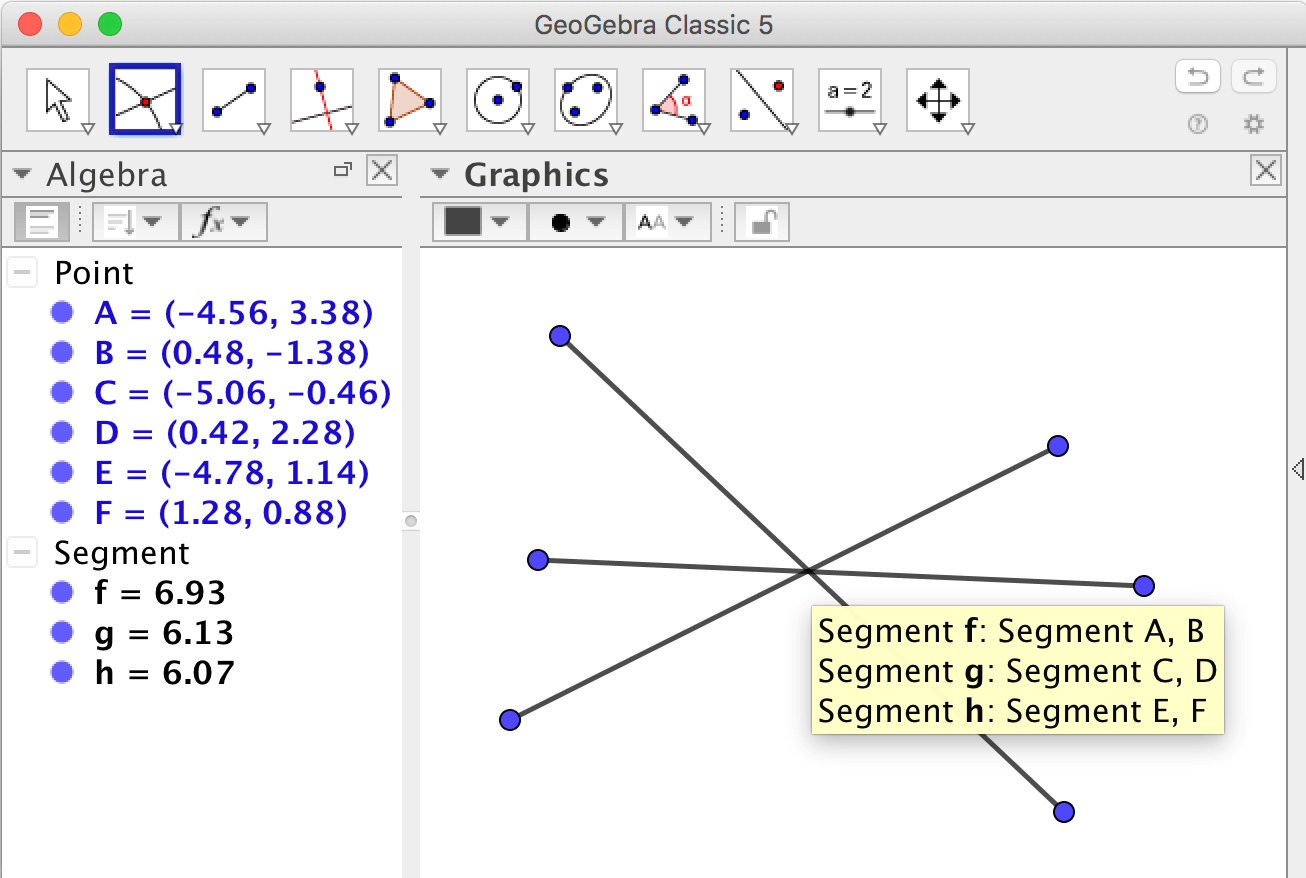
Om du som i bilden ovan har tre sträckor som skär varandra i ungefär samma punkt, så bör du inte klicka på den gemensamma skärningspunkten utan istället klicka två gånger med hjälp av verktyget Skärning mellan två objekt. Klicka först på den ena sträckan och sedan på den andra. Du kan klicka på sträckorna antingen i ritområdet eller i algebrafönstret.

Passare och linjal

Med en geometrisk konstruktion menas vanligtvis en konstruktion som görs enbart med en passare och en linjal. Här använder vi ordet konstruktion som en konstruktion vilken kan göras med alla GeoGebras verktyg.

Det går att använda GeoGebra till klassiska passare-och-linjal-övningar. Välj Verktyg - > Anpassa verktygsfält och välj ut de verktyg som motsvarar en klassisk passare och linjal.

Ladda GeoGebra-arbetsblad

För exempel på passare-och-linjal-övningar se Geometri ‐ Passare och linjal eller Geometri ‐ Omskrivna och inskrivna cirklar.

Övningar

Övning 1

Konstruera ett pentagram

• Gör en pentagon (en regelbunden femhörning)
• Dra sträckor mellan punkterna i pentagonen med verktyget Sträcka.
• Om du vill färglägga ett område måste du först göra det till en polygon. Skärningspunkterna mellan sträckorna måste därför användas som den nya polygonens hörnpunkter. Skapa de fem skärningspunkterna!
• Använd verktyget Polygon för att göra pentagrammet.
• Göm den ursprungliga pentagonen genom att högerklicka på den och avmarkera Visa objekt. Göm också de sträckor du inte vill visa. Notera att du inte kan ta bort pentagonen, den används i konstruktionen, du kan bara gömma den.

Nu ska du kunna flytta pentagrammet och ändra storlek genom att dra i punkterna A och B. Hur du än drar, ska det dock fortfarande vara ett pentagram. Det är detta som gör det till en konstruktion istället för en teckning.

Övning 2

Konstruera ett annat pentagram

Konstruera ett pentagram där de två punkter som alla övriga objekt beror på är placerade som i arbetsbladet nedan.

Ladda GeoGebra-arbetsblad

Du kan göra ett pentagram-verkty under menyn >Verktyg -> Skapa nytt verktyg.

Välj först pentagrammer som det färdiga objektet.

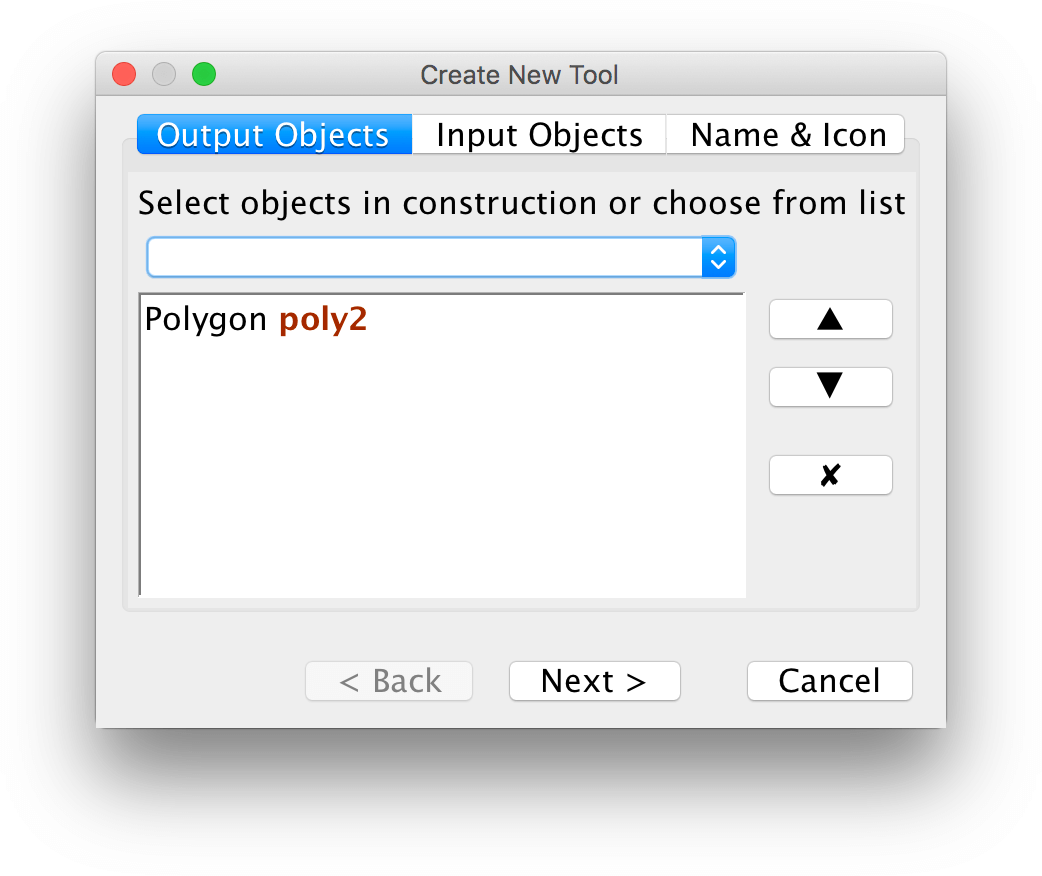
Välj sedan inmatningsobjekt. I det här faller är dessa redan valda.

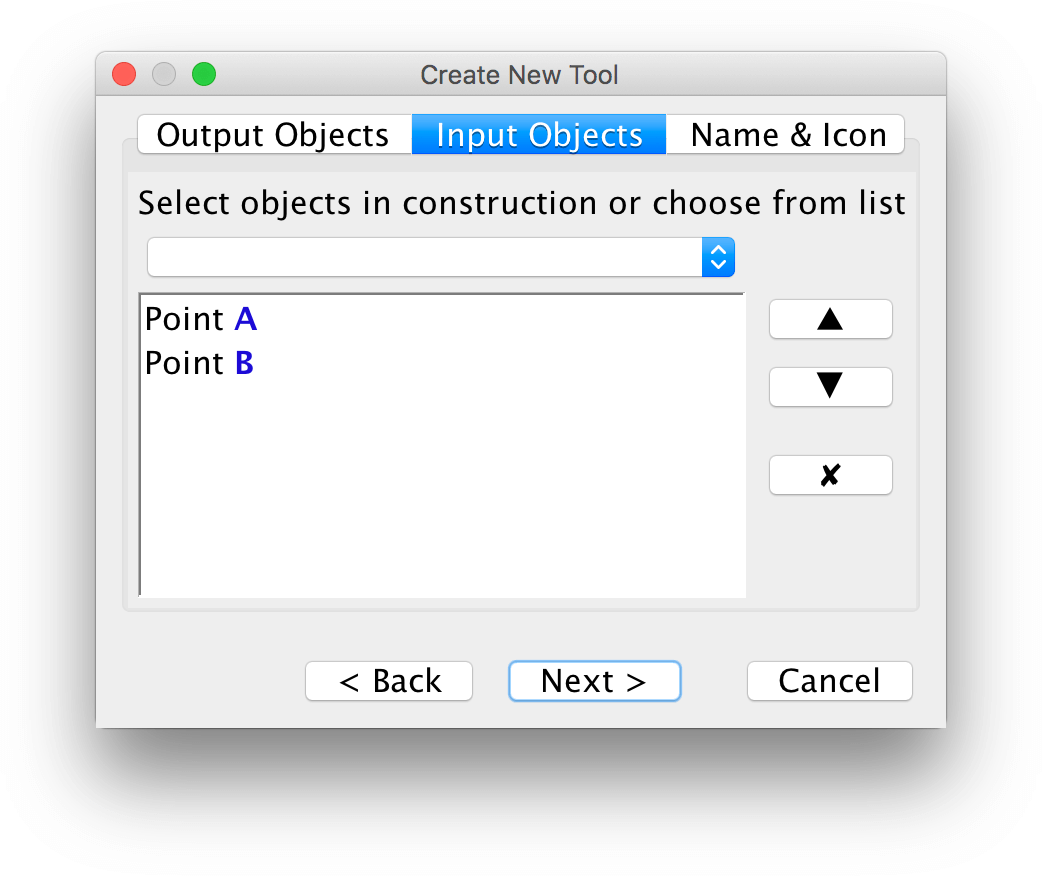
I det sista steget namnger du ditt verktyg. Du kan också använda en bild som verktygsikon.

Övning 3

Konstruera en parallellogram

Gör en parallellogram som en konstruktion. När konstruktionen är klar ska man kunna dra i punkterna för att förflytta och ändra utseendet; hur man än drar i punkterna ska det dock fortfarande vara en parallellogram ‐ konstruktionen ska klara dragningstestet.

Övning 4

Konstruktioner med cirklar

En cirkel har den makalösa egenskapen att alla punkter på cirkeln har samma avstånd till cirkelns mittpunkt. Denna egenskap används ofta vid konstruktioner.

• Gör en likbent triangel som en konstruktion. Se till att din konstruktion klarar dragningstestet.
• Gör en romb som en konstruktion. Se till att din konstruktion klarar dragningstestet.

Övning 5

Katt på stege

Du ska åskådliggöra en stege (mellan \(A\) och \(B\)) som står uppställd mot en vägg. Stegen ska kunna glida ned längs väggen. På det mittersta trappsteget (punkten \(C\)) sitter det en katt. När stegen glider ner från väggen följer katten en cirkulär bana.

Om stegen bara ska kunna glida längs den positiva \(y\)-axeln, kan du placera punkten \(A\) på en stråle.

Använd verktyget Cirkel definierad via medelpunkt och radie för att konstruera stegen.

Använd verktyget Mitt- eller medelpunkt för att placera katten.

När du är klar kan du visa kattens bana genom att:

1. lägga ett spår på punkten \(C\). Du kan sudda ut spåret genom att zooma eller flytta ritområdet.
2. använda verktyget Geometrisk ort. Klicka först på \(C\) och sedan på \(A\).

Om du vill visa en bild på en katt, kan du använda verktyget Infoga bild till att infoga bilder.

Ladda GeoGebra-arbetsblad

Övning 6

Flera katter på en stege

En katt som sitter någonstans på en stege, kommer att följa en elliptisk bana om stegen glider ner från väggen.

Konstruera en stege som i Övning 5 och placera flera katter på stegen, exempelvis genom att upprepade gånger använda verktyget Mitt- eller medelpunkt.

Istället för att göra en geometrisk konstruktion av stegen kan du använda trigonometri och en glidare \(t\) som representerar en vinkel. Hur kan stegens två ändpunkter skrivas som uttryck i \(t\) för att stegens längd ska vara konstant?

Om du vill kunna sudda ett spår på ett lite mer elegant sätt, kan du lägga in en knapp som zoomar med faktorn ett. På svenska använder du kommandot ZoomaIn(1).

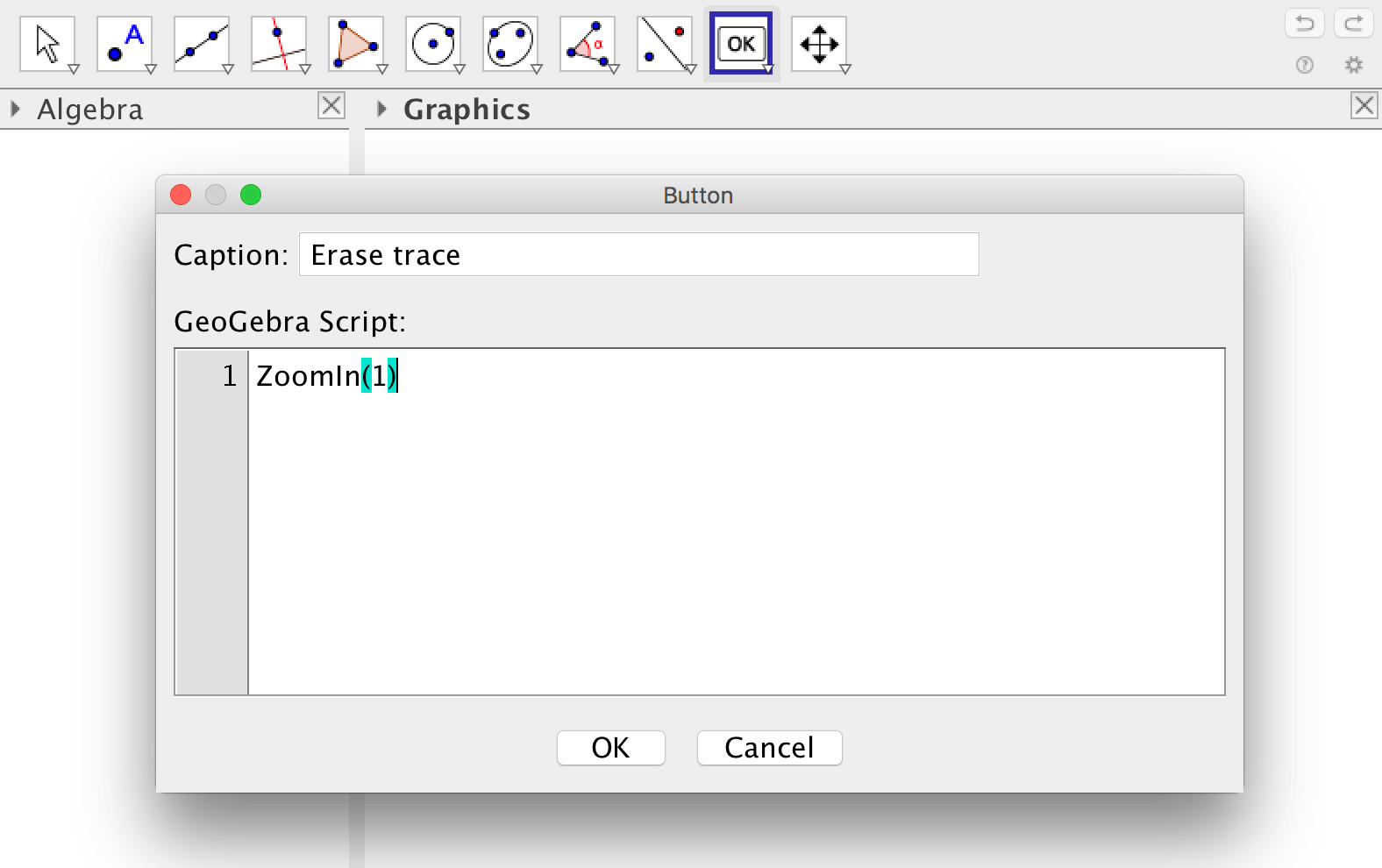
Vill du göra väldigt många objekt är det enklare att använda kalkylbladet, se Lär dig GeoGebra - Kalkylblad för mer information. Där visas också hur man använder dynamiska färger.

Ladda GeoGebra-arbetsblad

Övning 7

Peaucellier-Lipkins mekaniska länkning

Den första mekaniska länkningen i planet som omvandlar cirkulär rörelse till linjär rörelse (och vice versa), var den så kallade Peaucellier-Lipkin-länkningen som uppfanns 1864.

Länkningen kan modelleras i GeoGebra. En sådan modellering åskådliggörs nedan.

Ladda GeoGebra-arbetsblad

I bilden nedan visas några punkter som behövs. Man ska kunna dra i punkten \(C\) längs en cirkulär bana. Då ska punkten \(F\) röra sig längs en linjär bana.

Det finns tre avstånd i modellen som inte ändras när man drar i punkten \(C\). Det gäller att

Eftersom avstånden inte ska förändras hur man än drar i punkterna, bör du använda verktyget Cirkel(medelpunkt och radie) . De tre radier som behövs kan representeras av glidare.

Gör en interaktiv GeoGebra-modell av Peaucellier-Lipkin-länkningen på följande sätt:

Steg 1

Konstruera de tre första punkterna i modellen av länkningen, de punkter som i bilden heter \(A, B, C\). Man ska kunna dra i \(C\) utan att de andra två punkterna rör sig.

Steg 2

Konstruera de två punkter som i bilden heter \(D\) och \(E\). Dessa två punkter ska ha samma avstånd till punkten \(C\) och samma avstånd till punkten \(B\). Hur kan du åstadkomma en sådan konstruktion?

Steg 3

Konstruera den punkt som i bilden heter \(F\). Hur ska denna konstrueras så att \(CD = CE = DF = EF\)?

Steg 4

När konstruktionen fungerar kan du visa den cirkulära och den linjära banan genom att låta punkterna rita ut spår. Du lägger på ett spår genom att högerklicka på ett objekt och sedan välja Spår på.