Punkter och vektorer

Med GeoGebra skapar du ett objekt antingen genom a klicka på ett verktyg i verktygsfältet eller genom att skriva i inmatningsraden. Prova att skriva in följande i inmatningsraden:

B=(2,1) 

MinPunkt=(-1,2)

v=(2,2)

GeoGebra använder konventionen att:

Vektorer skrivs på matrisform i algebrafönstret. En vektor har en längd och en riktning, däremot ingen position. Lägg märke till att du kan flytta runt en vektor i GeoGebra utan att dess värde förändras

Ibland behöver man använda en punkts \(x\)- och \(y\)-koordinat. Om du har en punkt som heter \(A\), kommer du åt \(x\)- och \(y\)-koordinaten genom att skriva

Samma kommandon kan användas för vektorer.

En punkts koordinater kan användas till att göra nya punkter. Givet en punkt \(A\) kan du exempelvis att skriva in

B=(x(A),y(A)+1)

i inmatningsfältet för att skapa en punkt \(B\). Om du bara skriver

(x(A),y(A)+1)

skapas en punkt som får ett namn av GeoGebra.

Aritmetik

Om du multiplicerar en existerande vektor med en skalär i inmatningsfältet, skapas en ny vektor. Du kan också skapa nya vektorer genom att addera eller subtrahera två existerande vektorer.

Om du multiplicerar två existerande vektorer i inmatningsfältet skapas en variabel som har skalärprodukten som värde.

Samma aritmetik som kan användas för vektorer kan också användas för punkter. Beräkningarna utförs då på ortsvektorerna. Om \(A\) och \(B\) är två punkter så är deras ortsvektorer \(\vec{OA}\) och \(\vec{OB}\) de vektorer som startar i \(O\) (origo i detta fall) och pekar på respektive punkt.

Kommandon

Kommandona Punkt och Vektor kan användas till att skapa nya punkter/vektorer från existerande punkter/vektorer.

Givet en punkt \(A\) kan du skapa en vektor \(u\) med kommandot Punkt(A). Vektorn \(u\) skapas som ortsvektorn till \(A\).

Givet två punkter \(A\) och \(B\) kan du skapa vektorn från \(A\) till \(B\) med kommandot Vektor(A, B).

Givet en punkt \(A\) och en vektor \(v\), kan du skapa punkten \(C\) med kommandot Punkt(A,v).

Enhetsvektor

Givet en vektor \(u\) skapar du enhetsvektorn med kommandot Enhetsvektor(u).

Polära koordinater

Man kan ange en punkts position i ett koordinatsystem med hjälp av polära koordinater istället för med sedvanliga cartesiska koordinater. Om man använder polära koordinater, anger man punktens avstånd från origo, R, samt den vinkel punkten har med positiva x-axeln i moturs riktning, vinkeln α.

Om du högerklickar på en punkt i algebrafönstret kan du välja att visa de polära koordinaterna istället för de kartesiska. GeoGebra markerar att det är polära koordinater genom att använda semikolon som skiljetecken istället för komma.

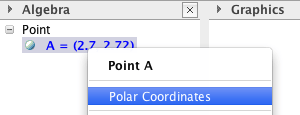
Om du vill skriva in en punkt i inmatningsraden genom att ange polära koordinater, skriver du in den med hjälp av semikolon.

	A=(2;30°)

Du hittar tecknet för grader i teckenmenyn bredvid inmatningsfältet. Du kan också klicka på Ctrl+O.

Övningar

Övning 1

Punkter och spår

• Se till att koordinataxlarna visa i ritområdet och gör en punkt \(A\). Skriv in

  B = (-x(A), y(A))

  i inmatningsfältet.

  Lägg ett spår på båda punkterna (högerklicka och markera Spår på), dra sedan runt punkten \(A\). De två punkterna kan ha olika färger. Spåret som ritas upp av \(B\) är en spegling i \(y\)-axeln av spåret som ritas upp av \(A\).

  Du suddar ut ett spår genom att zooma in eller ut, eller genom att flytta ritområdet genom att dra i det.

• Om punkten \(C\) skapas som

  C = (y(A), x(A))

  skapas en annan spegling av \(A\). Kan du beskriva speglingen utan att skapa \(C\)? Kolla om du hade rätt genom att skapa \(C\) i GeoGebra.

Övning 2

Samband och koordinater

I arbetsbladet nedan beror fem punkter på punkten \(A\).

Ladda GeoGebra-arbetsblad

Om du skriver in

(x(A)+3, y(A))

i inmatningsfältet i arbetsbladet, skapas en punkt som hamnar ovanpå den blå ihåliga punkten (inuti ringen).

Dra i punkten \(A\) och bestäm sambandet mellan koordinaterna för de andra punkterna. Skapa fyra nya punkter genom att skriva i inmatningsrutan. De nya punkterna ska hamna ovanpå de ihåliga punkterna (inuti varje ring).

Övning 3

Gör en koordinatövning

Gör en egen övning som liknar Övning 2.

För att göra arbetsbladet så användarvänligt som möjligt, kan du se till att musmarkören bara ändrar utseende då den är placerad på den punkt som ska kunna dras. Högerklicka på en punkt som inte ska kunna dras och visa Egenskapsfönstret. Under tabben Avancerat kan du avmarkera "Urval möjligt".

Övning 4

Parallellförflyttade kopior

Använd verktyget Vektor till att göra en vektor.

Skapa ett valfritt geometriskt objekt, exempelvis en polygon eller en cirkel.

Använd verktyget Parallellförflytta objekt med vektor till att göra flera parallellförflyttade kopior av det geometriska objektet.

Använd verktyget Flytta till att dra i de punkter som definierar vektorn.

Kommentar: Om du vill göra många kopior går det också att använda listor eller kalkylblad.

Övning 5

Addition av positiva och negativa tal med hjälp av slumptal

Ladda GeoGebra-arbetsblad

För att slumptalsgenerera ett positivt och ett negativt heltal, börjar du med att skapa två variabler. Skriv nr1 = 1 och nr2 = -1 i inmatningsfältet.

Använd verktyget Infoga knapp till att göra en knapp "Nya tal" och skriv följande GeoGebra-script:

SättVärde(nr1, SlumptalMellan(1, 7))
SättVärde(nr2, SlumptalMellan(-7, -1))

Du ska nu demonstrera addition med hjälp av vektorer och tallinjer. För att demonstrera att \(nr1+nr2 = nr2+nr1\), behöver du två tallinjer.

• Gör två linjer parallella med \(x\)-axeln vid \(y = 2\) och \(y = -2\). Du kan antingen skapa linjerna med verktyg, eller helt enkelt genom att skriva y = 2 och y = -2 i inmatningsfältet.

• Skapa vertikala sträckor längs linjerna med hjälp av listor av sträckor. Gör en lista med kommandot:

  Talföljd(Sträcka((i, 2.2), (i, 1.8)), i, -20, 20)

  Gör sträckor för den andra linjen på liknande sätt.

• Lägg dit värden för positionerna längs tallinjerna genom att göra en lista av text-element. Kommandot Text( <Objekt>, <Punkt> ) skapar ett textobjekt vid en punkt. Genom att använda ett femte argument till talföljdskommandot, kan du ange att steg. Skriv:

  Talföljd(Text(i, (i - 0.3, -0.2)), i, -20, 20, 5)

  Justera positionerna så att det ser bra ut.

• Gör två listor till med sträckor som är något längre men som bara visas vid multipler av fem.

Lägg till punkter som representerar talen vid tallinjerna, eller något ovanför eller under en tallinje. Gör vektorer mellan punkterna. Lägg till dynamisk text och andra objekt som hjälper till att visualisera additionen.