Symmetrier

Det finns tre transformationer som inte förändrar ett objekts storlek eller form. Att storleken och formen inte förändras innebär att alla avstånd och alla vinklar bevaras. Med andra ord är det transformerade objektet kongruent med det ursprungliga objektet. De tre transformationerna är:

En bild är symmetrisk om du kan utföra någon av dessa transformationer på bilden utan att bilden förändras. Bilden sägs då ha en spegelsymmetri, en rotationssymmetri eller en translationssymmetri. En bild kan innehålla flera symmetrier samtidigt.

Ladda GeoGebra-arbetsblad

För att en bild ska kunna vara translationssymmetrisk, måste man tänka sig att bilden fortsätter i oändligheten. Endast en bild med oändlig utbredning kan förbli oförändrad efter en parallellförflyttning. Ett exempel på en translationssymmetrisk bild är en tesselering.

Ladda GeoGebra-arbetsblad

Använd kommandon

Kommandona för att rotera runt en punkt, spegla i en linje, och parallellförflytta längs en vektor, är:

Rotera( <Objekt>, <Vinkel>, <Punkt> )
Spegla( <Objekt>, <Linje> )
Flytta( <Objekt>, <Vektor> )

Kommandon är speciellt användbara när du vill göra många transformationer med hjälp av listor eller kalkylblad.

Övningar

Övning 1

Regelbundna polygoners symmetrilinjer

Gör en glidare \(n\) som betecknar antal hörn.

Nu kan du använda verktyget Regelbunden polygon till att göra en polygon med \(n\) hörn. Om du använder samma två fixa punkter för att skapa alla polygoner, kommer de att variera för mycket i storlek. Gör istället så här:

• Gör en punkt \(O\) i origo och en punkt \(A\) med koordinaterna \((1, 0)\).

• Använd verktyget Rotera objekt runt punkt med vinkel till att rotera \(A\) runt \(O\) med vinkeln \(\dfrac{360^\circ}{n}\). En punkt \(A'\) skapas.

• Skapa polygonen med hjälp av \(A\) och \(A'\).

Nu ska polygonen speglas i en linje och användaren ska kunna undersöka hur många linjer man kan spegla polygonen i utan att bilden förändras.

Lägg in en vinkelglidare \(\alpha\) och rotera punkten \(A\) runt \(O\) vinkeln \(\alpha\). Döp den roterade punkten till \(B\) och gör en linje \(r\) genom \(O\) och \(B\). Spegla polygonen i linjen med verktyget Spegla objekt i en linje.

För att man nu enkelt ska kunna räkna antalet symmetrilinjer, kan du lägga in två knappar Stämpla och Sudda. Använd verktyget Infoga knapp. Skriv in GeoGebra-scriptet

ZoomaIn(1)

för Sudda-knappen och scriptet

SpårPå(r, true)
SpårPå(r, false)

för Stämpla-knappen.

Ladda GeoGebra-arbetsblad

Övning 2

Reflektera en triangel i linjen \(y=x\)

Att reflektera en triangel i en vertikal eller horisontell linje är ganska lätt. Att reflektera i linjen \(y=x\) är något svårare.

För en övning där användaren ska dra i hörnen av en triangel för att bestämma en "korrekt triangel", är det bäst att låsa positionerna till rutnätet i stilmenyn.

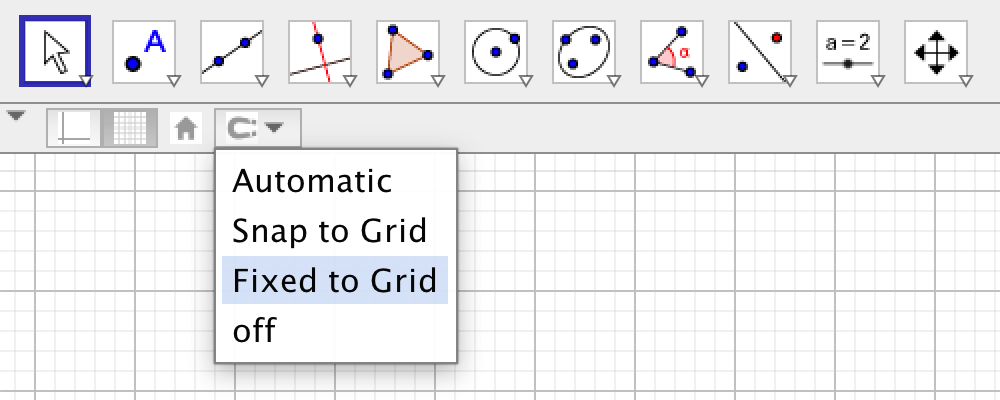
Skapa linjen \(y = x\) och en valfri triangel. Göm punkterna som definierar triangeln. Markera triangeln och klicka på "Lås objekt" i stilmenyn.

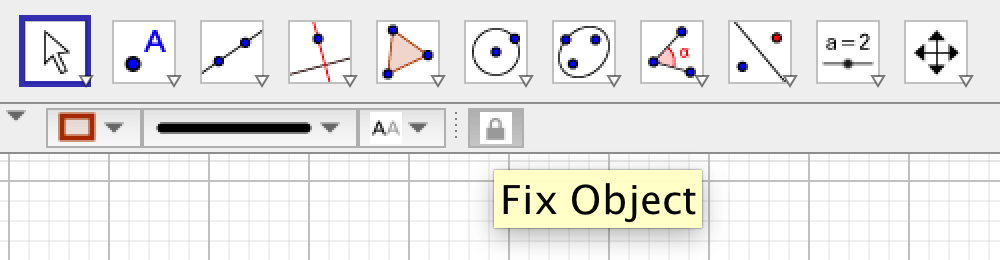
Skapa en annan triangel, en triangel vars hörn användaren ska kunna dra.

Användarens uppgift är att se till att trianglarna är varandras spegling i linjen. Och att sedan kontrollera om det blivit rätt genom att använda verktyget Spegla objekt i en linje.

Du kan välja vilka verktyg som ska visas i menyn Verktyg -> Anpassa verktygsfält.

Ladda GeoGebra-arbetsblad

Kommentar: Liknande övningar kan göras där användaren ska rotera något objekt \(90^\circ\) eller \(180^\circ\) runt en punkt.

Övning 3

Gör en tesselering

• Gör en triangel.
• Lägg in en vektor \(\vec{u}\) som går mellan två hörn i triangeln och en vektor \(\vec{v}\) som går mellan två andra hörn.
• Använd verktyget Parallellförflytta objekt med vektor och gör en kopia av triangeln längs vektorn \(\vec{u}\) och en kopia längs vektorn \(\vec{v}\).
• Gör fler kopior av de nygjorda trianglarna.
• Dra i punkterna som utgör hörn i den första triangeln, hela tesseleringen ändrar sig.
• Om du vill färglägga områdena mellan trianglarna kan du göra en ny triangel på något ställe som täcker det vita mellanområdet; sedan parallellförflytta denna nya triangel med hjälp av vektorerna \(\vec{u}\) och \(\vec{v}\).

Övning 4

Skapa rotationssymmetri med hjälp av listor

Gör en glidare \(n\) för antalet rotationer.

Gör en triangel och döp om den till \(t\).

För att skapa \(n\) roterade kopior av triangeln, där rotationen är runt origo, skriver du

Talföljd(Rotera(t, i*2pi/n), i, 1, n)

i inmatningsfältet (jo, "talföljd" är ett märkligt ord i detta sammanhang).

Göm den ursprungliga triangeln. Dra i punkterna och ändra värde på \(n\).

Listan du nu skapat är ett enda objekt. Du kan ge listan en färg men du kan inte färglägga de olika listelementen med olika färger. Vill du att trianglarna ska ha olika färg, kan du använda kalkylbladet istället.

Ladda GeoGebra-arbetsblad

Övning 5

Skapa en tesselering med hjälp av listor

Gör en regelbunden triangel med hjälp av punkterna \((0,0)\) och \((1,0)\). Göm triangeln och se till att punkterna \(A, B, C\) är låsta objekt (så man inte kan dra i dem).

Gör sex punkter till, placerade ungefär längs den gömda triangelns sidor. Gör en polygon av dessa nio punkter. Döp om polygonen till \(p\).

Gör två translationsvektorer \(\vec{u} = \vec{AB}\) och \(\vec{v} = \vec{AC}\).

Skapa en lista av translaterade kopior med hjälp av den ena vektorn:

Talföljd(Flytta(p, i*u), i, -5, 5)

En lista \(Lista_1\) skapas. Göm den.

Gör en lista av translaterade kopior av \(Lista_1\) längs den andra vektorn:

Talföljd(Flytta(Lista_1, i*v), i, -5, 5)

Göm vektorerna och den ursprungliga polygonen. Dra i punkterna.