Dynamisk text, mätning och dekorationer

Dynamisk programvara fungerar väl för att hitta matematiska mönster. Genom att undersöka numeriska värden är det möjligt att dra slutsatser, slutsatser som sedan bevisas som det sista steget i en matematisk undersökning.

wheelParadox — Aristoteles hjulparadox. En påminnelse om att en slutsats som dras utifrån en visualisering måste åtföljas av ett matematiskt resonemang.

När GeoGebra används för att undersöka numeriska samband, eller när du som lärare vill demonstrera ett numeriskt samband, är ett enkelt tillvägagångssätt att studera värden i algebrafönstret eller värden som visas som etiketter bredvid ett objekt. Du kan själv välja hur en etikett ska visas, högerklicka på ett objekt och välj Egenskaper.

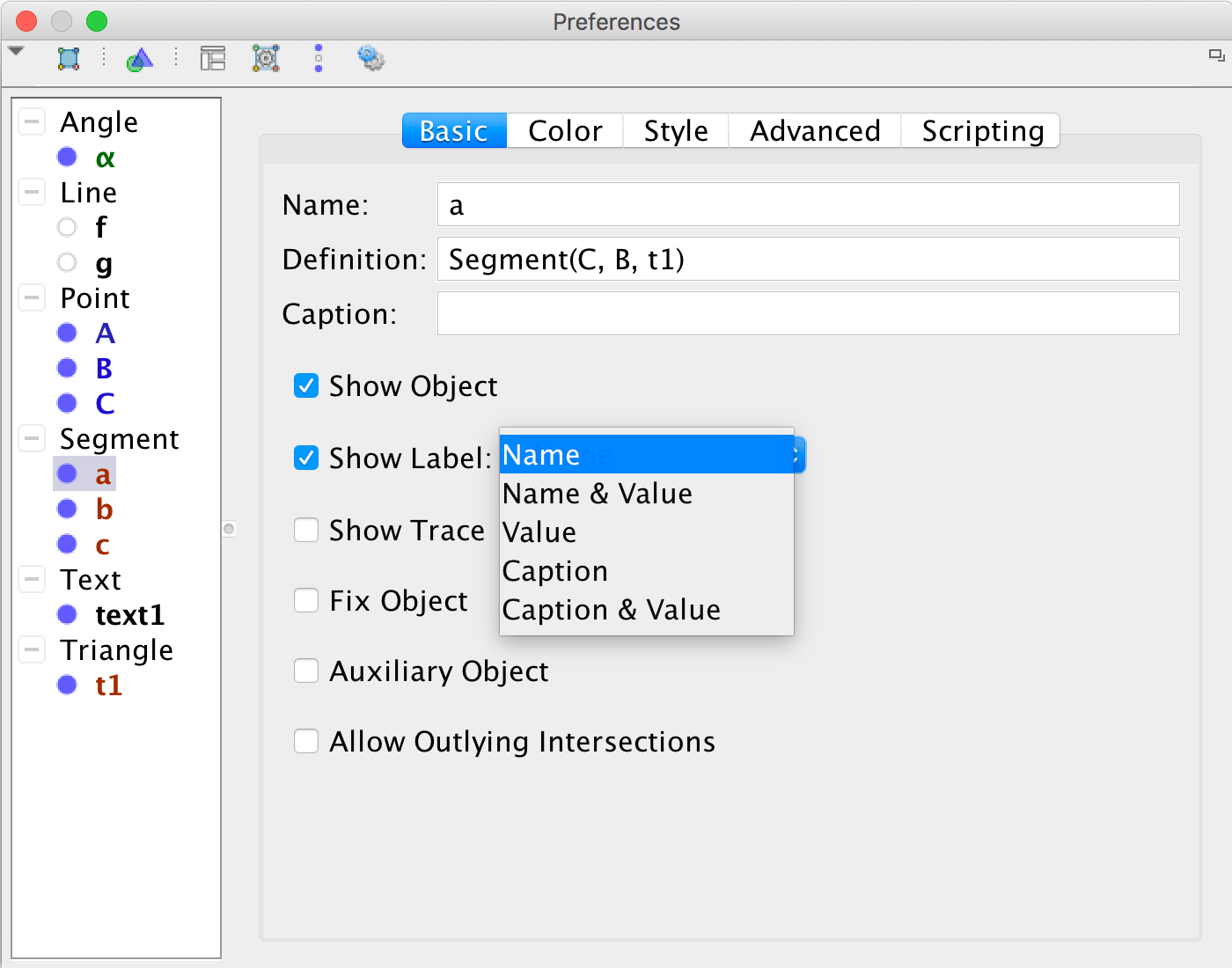
Det kan vara svårt att se vad det är som händer, och att utröna om det finns ett numeriskt samband, genom att bara studera etiketter eller värden i algebrafönstret.

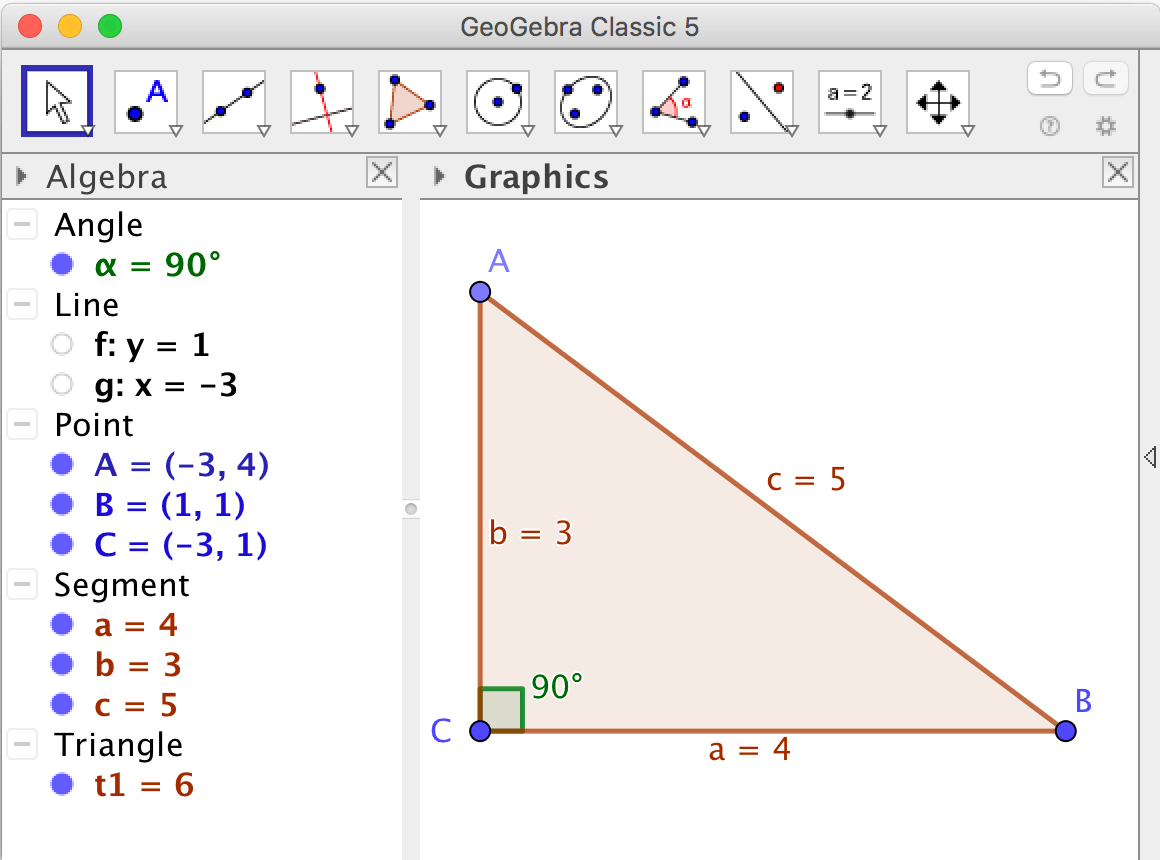
Pythagoras 1 — Det är svårt att se det numeriska sambandet när punkterna dras runt.

Av den anledningen är det oftast en bra idé att visa numeriska samband med hjälp av dynamisk text.

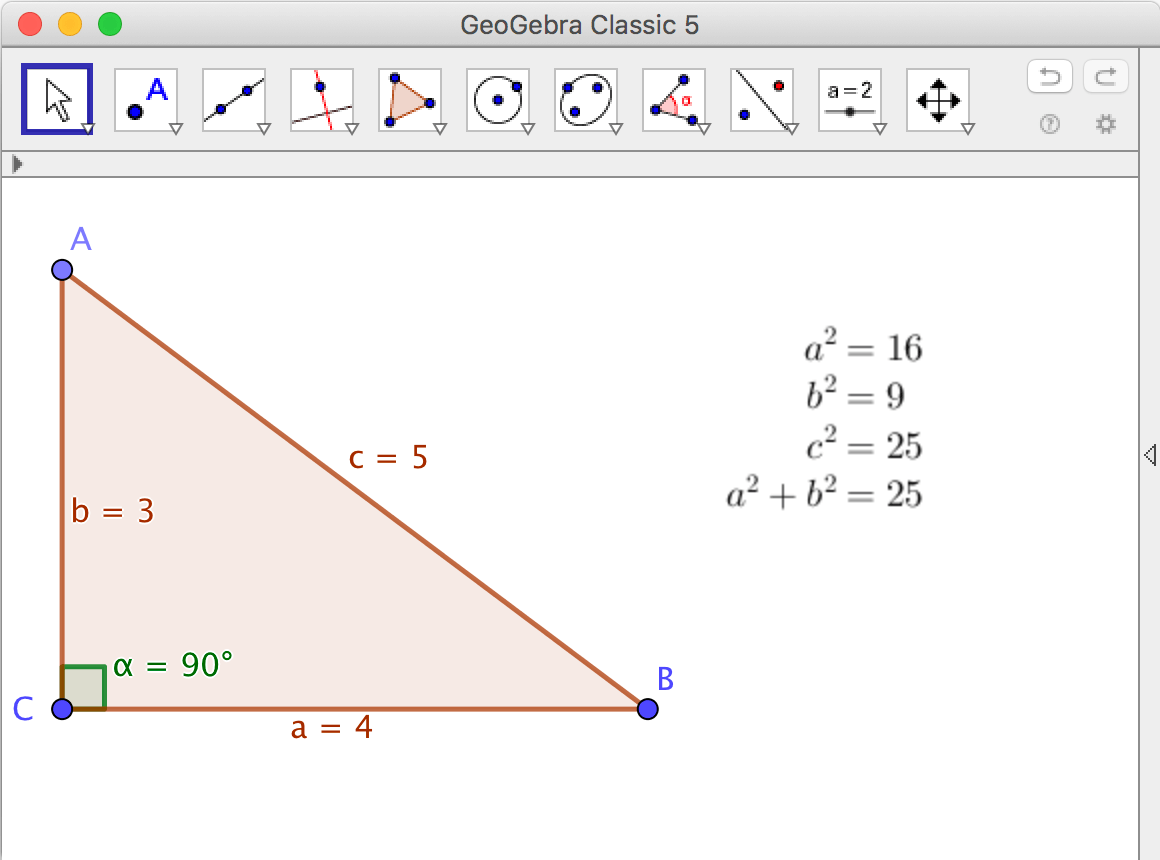
Pythagoras 2 — Det numeriska sambandet blir tydligt med dynamisk text.

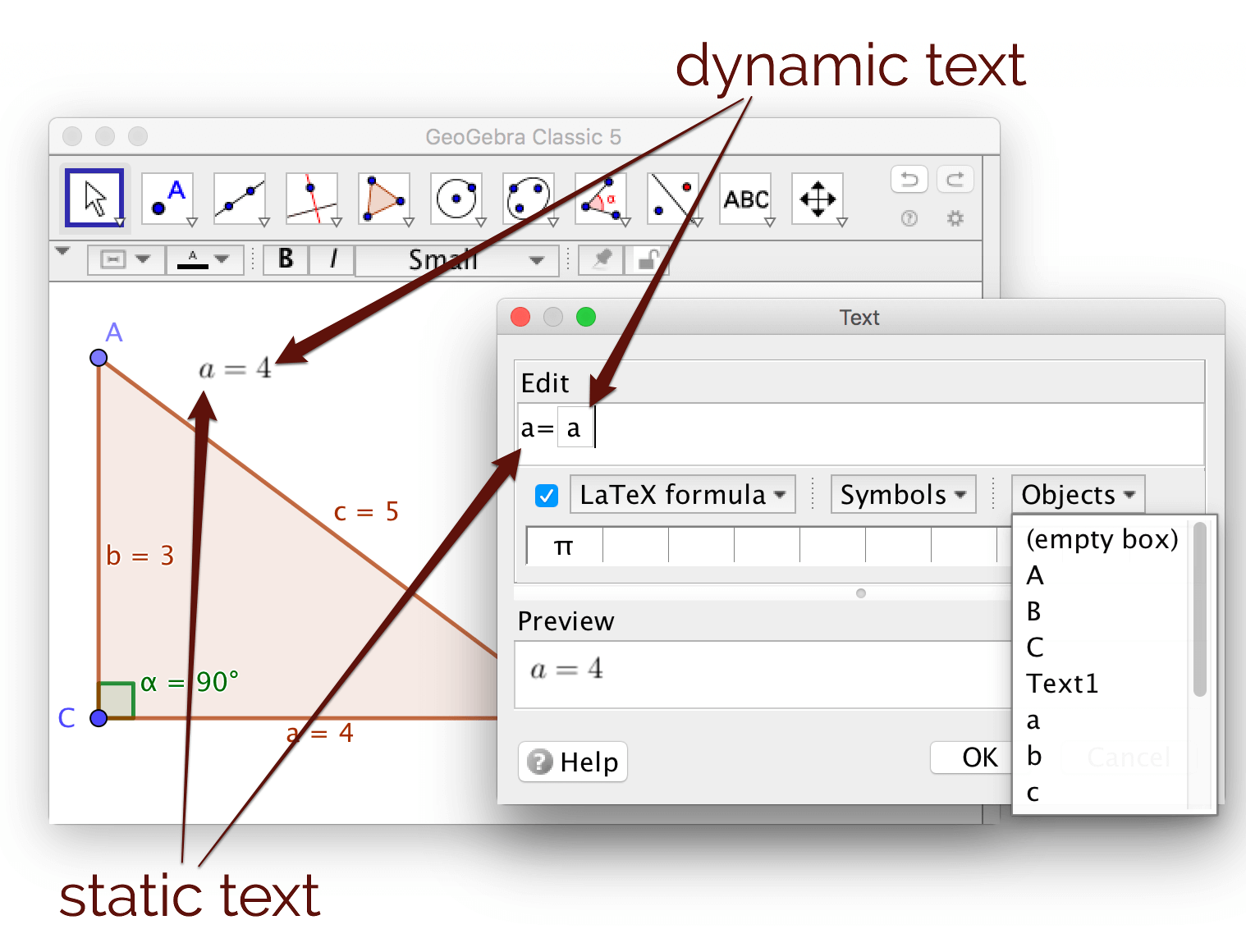
Statisk och dynamisk text

Om du vill visa text, klickar du på verktyget Infoga Text , och klickar sedan i ritområdet. Om du vill visa värdet av ett objekt, klickar du på menyn Objekt och väljer ett objekt. Detta objekt visas inuti en ruta i redigeringsytan. När värdet på objektet förändras, genom att du drar i punkter, så förändras även det värde som visas ‐ den visade texten är dynamisk.

LaTeX i GeoGebra

Det vanligaste sättet att skriva matematik är att använda LaTeX och TeX-syntax för formler. LaTeX används av GeoGebra och du måste inte kunna mycket TeX-syntax för att använda det. För att använda LaTeX markerar du LaTeX-formel i textediteringsrutan. Om GeoGebra känner igen det du skriver som TeX-kod, kommer LaTeX-formel automatiskt att markeras.

Även om du inte kan LaTeX, eller vill lära dig LaTeX, bör du veta hur man skriver upphöjda och nedsänkta tecken.

Upphöjt skrivs med hjälp av ^ x^2 skrivs ut så här \(x^2\)

Nedsänkt skrivs med hjälp av _ c_1 skrivs ut så här \(x_1\)

Samma tecken (^ och _) används för variabelnamn i GeoGebra. Du skriver tecknet ^ genom att trycka Shift+^. Tecknet ^ visas eventuellt inte förrän du trycker ner nästa tangent eller trycker på spacebar. Du skriver tecknet _ genom att trycka Shift+-.

Om du inte kan LaTeX får du en viss hjälp från GeoGebras textediteringsruta. Markera LaTeX-formel och välj en formel från meny som visas vid den lilla svarta pilen. Klicka på den formel du vill använda. I efterhand kan du byta ut de bokstäver som genererats till de bokstäver du vill använda.

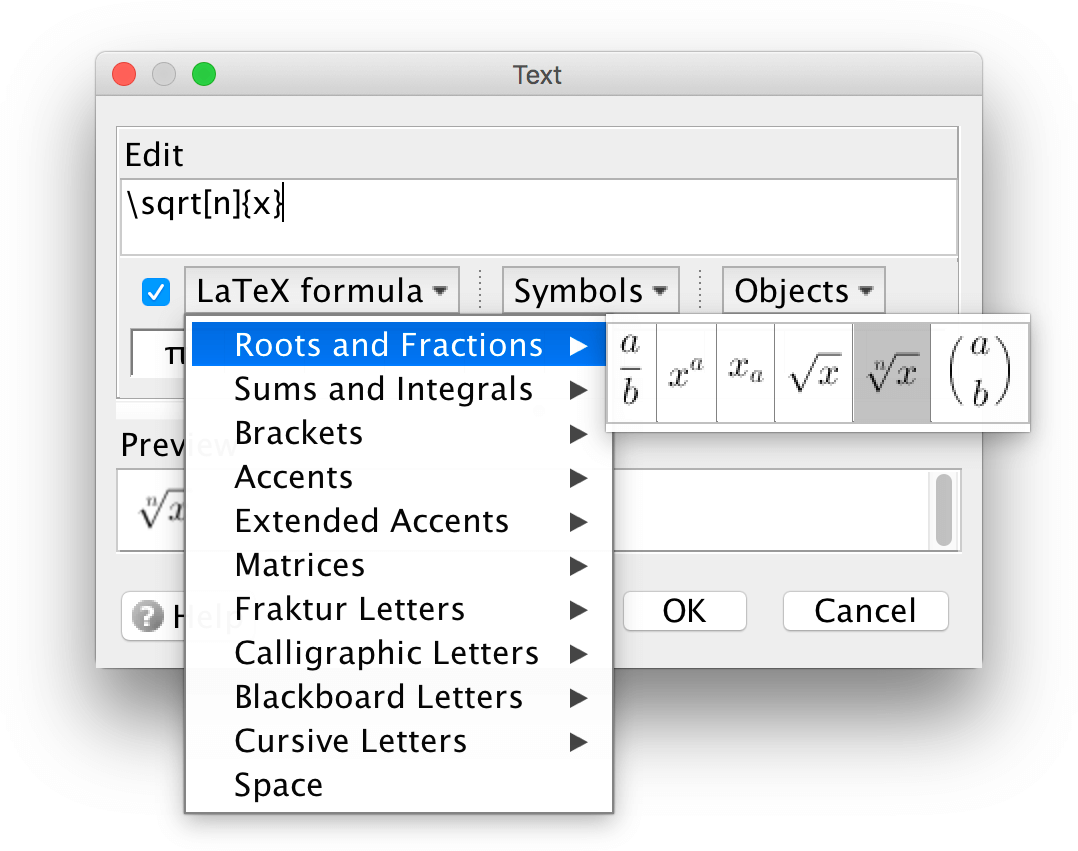
Objektuttryck

När du vill visa värdet av ett objekt klickar på Objekt-menyn och väljer ett objekt. Objektet visas inuti en liten ruta. Inuti denna lilla rita kan du skriva matematiska uttryck med de objekt som du skapat.

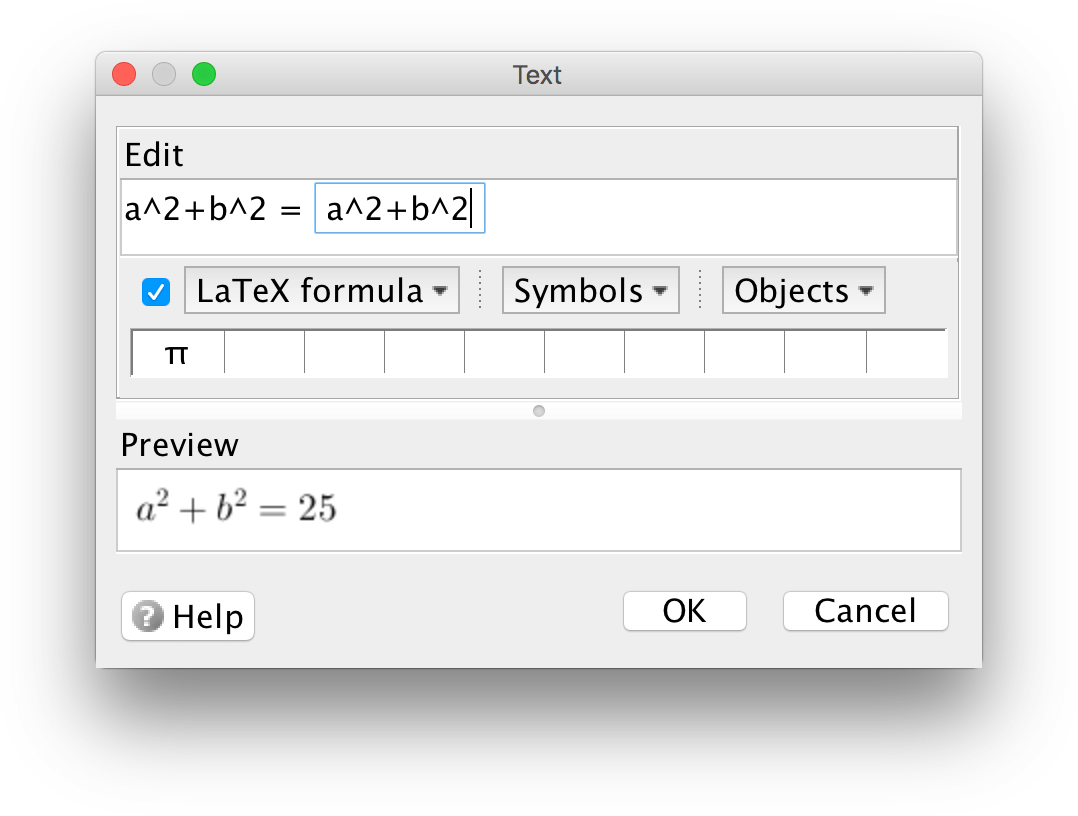
Vanlig text och LaTeX

Då man skriver formler i LaTeX, kursiveras texten och blanktecken ignoreras. Av den anledningen blir resultatet inte alltid som förväntat då en formel formateras till LaTeX.

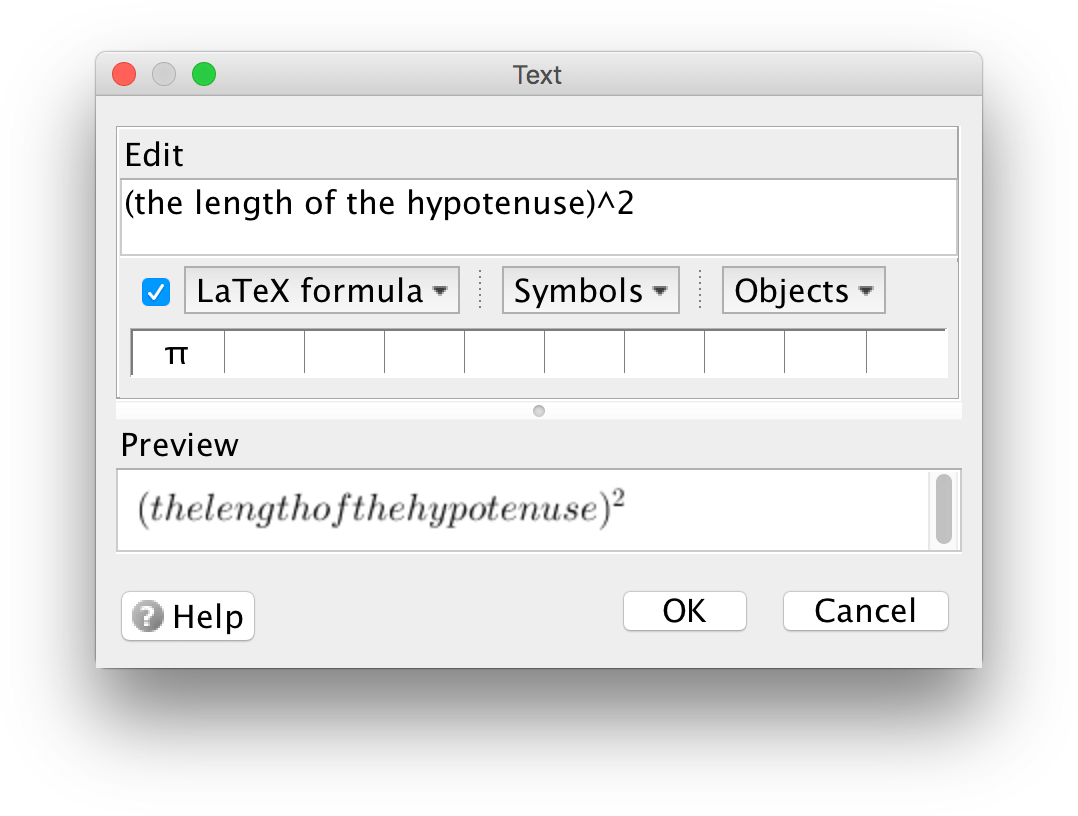
Om du vill skriva vanlig text i en LaTeX-formel, dvs med blanktecken och icke-kursiverad, kan du innesluta den vanliga texten mellan måsvingarna i kommandot \text{}.

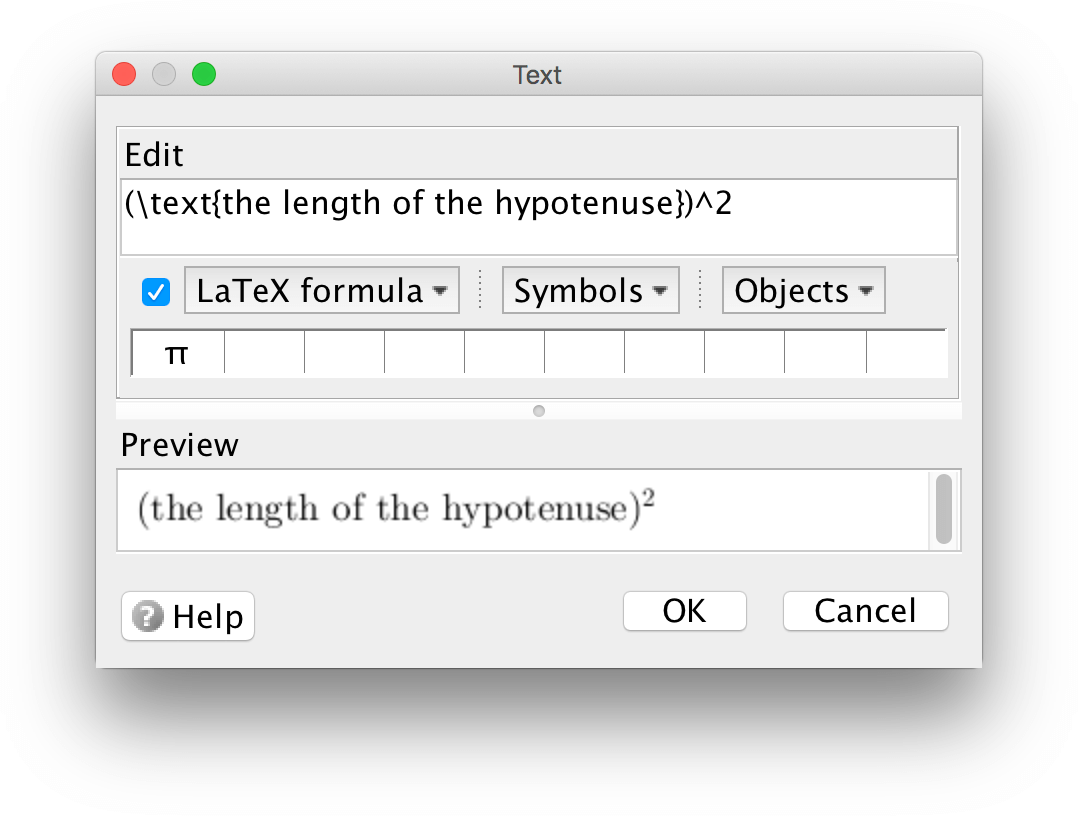
Mätning

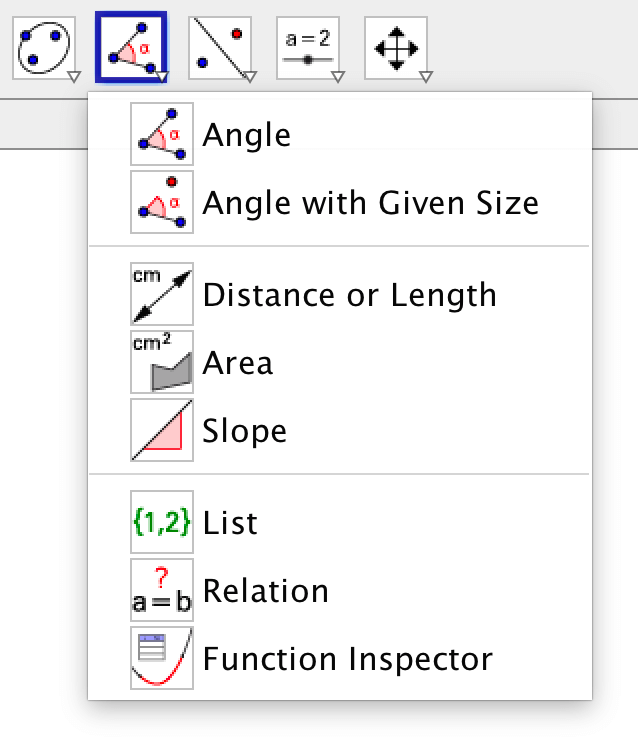
I verktygsraden finns det en meny med verktyg för att mäta objekt.

Lägg märke till att om du håller musen över ett verktyg står det vilka objekt verktyget behöver. Ska du mäta en vinkel måste du antingen klicka på tre punkter eller på två linjer/segment.

Med hjälp av verktygen kan du mäta vinklar, areor, längder och lutning. Varje sak du mäter lagras i en variabel som syns i algebra-fönstret och dessutom skapas en textruta där det uppmätta värdet visas. Notera att texten ändras dynamiskt då de uppmätta objektens värden ändras.

Enheter

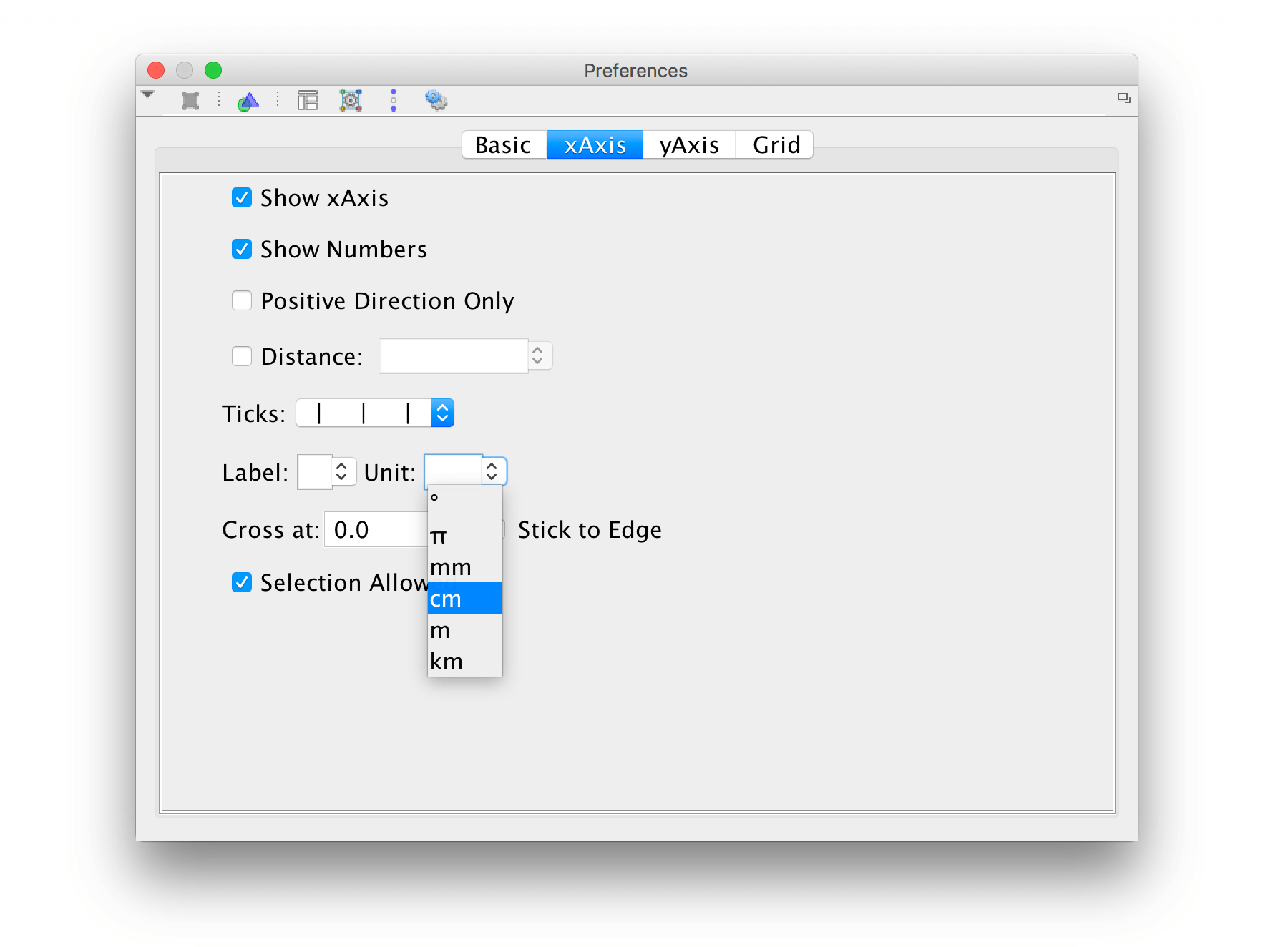
Du kan visa enheter längs koordinataxlarna. Klicka på hjul-ikonen för "Inställningar" i det övre högra hörnet och välj "Ritområde".

Det finns en flik för x-axeln och en flik för y-axeln.

Mätning med ett kommando

Alla objekt du kan skapa med verktygen i verktygsraden, kan du också skapa genom att skriva in ett kommando i inmatningsraden. Alla kommandon verkar på ett eller flera objekt, dessa måsta anges som argument till kommandot. Du skriver in argumenten innanför parenteser.

Alla kommandon finns i en lista som visas om du klickar på ikonen till höger om inmatningsraden. Om du klickar på ett kommando får du veta vilken sorts argument kommandot har.

Vill du mäta exempelvis ett avstånd, skriver du Av, därefter visar GeoGebra en lista med kommandon som börjar på Av. Välj ett förslag ur listan genom att använda piltangenter, klicka därefter på Enter. GeoGebra fyller i resten av ordet och markören hamnar innanför parenteserna. Därefter skriver du in namnen på de objekt du vill mäta avståndet mellan.

Det skapas nu en ny variabel där avståndet lagras, variabeln syns i algebrafönstret; däremot så skapas det ingen textruta som visar det uppmätta värdet.

Mäta vinklar

Vinklar namnges i GeoGebra med grekiska bokstäver. Då du mäter en vinkel mellan tre punkter, finns det två tänkbara vinklar som visas, beroende på om du anger punkterna medurs eller moturs. Om du inte får den vinkel dy vill visa, kan du antingen ångra med Cmd/Ctrl+z eller genom att klicka på ångra-ikonen i det övre högra hörnet.

I egenskapsfönstret kan du välja att alltid visa en vinkel inom något intervall.

För att skriva symbolen för grader klickar du på Ctrl+O!

angles — Dra i de blå punkterna för att se andra vinklar.

Utöver de vanliga egenskaperna, så som färg och storlek, kan du också använda dekorationer.

Dekorationer

När GeoGebra används till interaktiva arbetsblad kan du visa samband för vinklar eller sträckor genom att visa deras värden. Det går också att visa likhet genom att dekorera vinklar eller sträckor. Dekorationer är speciellt användbara för statiska bilder.

decorations — Lika vinklar/sträckor är dekorerade på samma sätt.

Du hittar de dekorationer som kan användas under Utseende-tabben i Egenskapsfönstret.

Övningar

Övning 1

Gör en demonstration av Pythagoras sats

Konstruera en rätvinklig triangel med följande verktyg:

Linje

Vinkelrät linje

Punkt

Polygon

Se till att din konstruktion klarar dragningstestet och göm objekt som inte ska synas.
Döp om triangelsidorna så att kateterna kallas \(a\) och \(b\) och hypotenusan \(c\). Markera också den räta vinkeln med hjälp av verktyget Vinkel.
Använd dynamisk text till att visa numeriska värden som antyder att Pythagoras sats möjligen kan vara sann.

Kommentar: Denna konstruktion är in till någon hjälp när det handlar om att förstå varför Pythagoras sats är sann. Det går också att göra konstruktioner som fungerar som förklaringar. Två sådana konstruktioner visas på sidan Geometry ‐ Pythagoras & Thales.

Övning 2

Demonstrera randvinkelsatsen

Gör en cirkel med verktyget Cirkel (medelpunkt och periferipunkt). Placera tre punkter på cirkeln. Använd verktyget Vinkel till att visa randvinkeln och medelpunktsvinkeln. Lägg till dynamisk text som demonstrerar randvinkelsatsen. Dra i de tre punkterna!

Kommentar: Eftersom denna konstruktion är relativt enkel är den ett bra exempel på en konstruktion som lämpar sig som elevaktivitet snarare än lärardemonstration.

by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License

www.malinc.se

◄ Konstruktioner

Punkter och vektorer ►