Kalkylblad

Kalkylbladet i GeoGebra har nästan alla egenskaper som vanliga kalkylblad har. När det bara handlar om numeriska beräkningar är sedvanliga kalkylblad bättre än GeoGebras. Det objektorienterade sätt som GeoGebra är uppbyggt på, gör emellertid GeoGebras kalkylblad till ett mycket kraftfullt verktyg. Bortsett från tal och formler, kan du också hantera alla GeoGebra-objekt i kalkylbladet.

Om du behöver många objekt som följer något mönster, kan du använda kalkylbladet.

Ladda GeoGebra-arbetsblad

Relativa kopior

Ett kalkylblad är en tabell av så kallade celler. Varje cell namnges med en bokstav (efter kolumnen) och ett tal (efter raden).

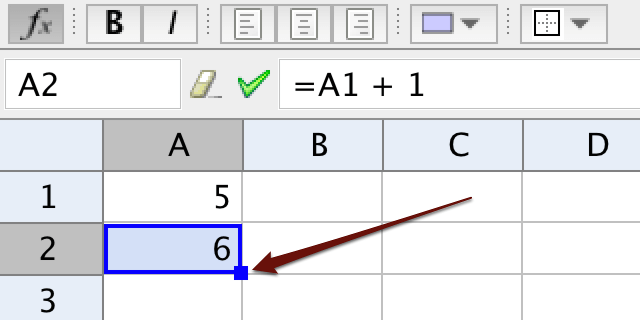
Den grundläggande funktionaliteten för kalkylblad är att du kan göra relativa kopior genom att dra en cell, eller genom att dra flera celler. Efter att du valt en cell, eller flera celler, visas en ifylld blå rektangel i det nedre högra hörnet av markeringen. Det är genom att dra i denna ifyllda rektangel som du gör relativa kopior.

Om cell A1 innehåller värdet 5 och du skriver in uttrycket A1 + 1 i cell A2, så hämtas värdet för A1 från den relativa placeringen, dvs från cellen ovanför. När du drar A2 neråt för att göra relativa kopior, kommer varje cell att hämta värde från cellen ovanför och addera detta med ett.

Absoluta referenser

Du kan använda dollartecknet för att göra absoluta referenser när du kopierar.

Genom att skriva $A1, gör du en absolut referens till A1 när du drar längs en rad.

Genom att skriva A$1, gör du en absolut referens till A1 när du drar längs en kolumn.

Genom att skriva $A$1, gör du en absolut referens till A1 när du drar både längs en rad och en kolonn.

Absoluta referenser kan användas för att skapa en multiplicationstabell.

Skapa objekt med kalkylbladet

Du kan skapa objekt i kalkylbladet genom att skriva ett kommando i en cell. Om du behöver hjälp med kommandot bör du skriva det i kalkylbladets inmatningsfält.

Dynamiska färger

Om du högerklickar på ett objekt och betraktar egenskapsfönstret, kan du se en rubrik Dynamiska färger under tabben Avancerat. Här kan du specificera hur mycket rött, grönt, och blått objektets färg ska bestå av. Varje värde ska vara ett tal mellan 0 och 1. Du kan skriva logiska uttryck för att ange färgerna, eller låta en färgs värde bero på en variabel, därav rubriken dynamiska färger. Med kalkylbladet kan du låta ett objekts färg bero på värdet i någon cell. När du gör relativa kopior kommer också färgen att kopieras relativt.

Skapa funktioner med kalkylbladet

Om du skriver ett uttryck i variabeln \(x\), kommer GeoGebra att skapa en funktion av \(x\). Genom att skriva sådana uttryck i celler i kalkylbladet, kan du skapa funktioner.

Övningar

Övning 1

Linjär och exponentiell löneförhöjning

• Lägg in en glidare \(a\) med heltalsvärden mellan 0 och 10 000 som representerar hur mycket Annas månadslön ökar per år i kronor.

• Lägg in en glidare \(b\) med heltalsvärden mellan 0 och 100 som representerar hur många procent Bertil månadslön ökar med per år i kronor.

• Lägg in år och månadslön för Anna och Bertil i ett kalkylblad och gör relativa kopior för att visa löneutvecklingen över ett antal år. Antag att de startar med samma lön år noll.

  

• Skapa en punktlista för Anna och en för Bertil. Markera celler från två kolumner och högerklicka, välj sedan Skapa - > Lista med punkter.

  Dra i \(y\)-axeln tills du ser punkterna i ritområdet.

• Dra i glidarna för att se olika löneutvecklingar.

Övning 2

Parabel

På antiken var koordinatsystem och funktioner ännu inte uppfunna och en parabel var ett geometriskt objekt som kunde definierades så här:

Givet en linje (kallad direktris) och en punkt (kallad brännpunkt) är en parabel mängden av de punkter som har samma avstånd till punkten som till linjen.

En punkt \(P\) som har samma avstånd till punkten som till linjen måste ligga på mittpunktsnormalen mellan punkten och någon punkt på linjen. Man kan visa att mittpunktsnormalen är tangent till parabeln genom \(P\). Mittpunktsnormaler kan därför användas för att åskådliggöra en parabels form.

Del 1

Gör en punkt \(A\) och en linje mellan två andra punkter \(B\) och \(C\). Placera fjärde punkt \(D\) på linjen och skapa mittpunktsnormalen mellan \(A\) och \(D\).

Lägg ett spår på mittpunktsnormalen och dra i \(D\).

Del 2

Istället för att använda spår ska du nu skapa ett antal punkter på linjen och ett antal mittpunktsnormaler.

• Ta bort spåret från mittpunktsnormalen.
• Placera en punkt \(E\) på linjen och skapa en vektor \(\vec{u}\) från \(D\) till \(E\).
• Döp om \(D\) till \(A1\) och \(E\) till \(A2\). Då hamnar de i kalkylbladet.
• Skriv in A2 + u i cell A3 och gör relativa kopior längs kolumn A.
• Skriv in Mittpunktsnormal(A1, A) i cell B1 och gör relativa kopior längs kolumn B.
• Ändra på brännpunkten och direktrisen, då ska alla mittpunktsnormalet också förändras.

Ladda GeoGebra-arbetsblad

Kommentar: På ett liknande sätt kan man göra mittpunktsnormaler mellan en punkt och punkter på en cirkel, detta visas i arbetsbladet överst på sidan.

Övning 3

Diskret modell av hund som jagar hare

En hare springer längs en flod. I modellen startar haren i origo och springer uppåt längs \(y\)-axeln.

En hund får syn på haren och börjar jaga den. I modellen startar hunden någonstans på positiva \(x\)-axeln.

Hunden springer en sträcka, tittar sedan upp och ser harens nya position och ändrar riktning, därefter springer den en sträcka till, osv.

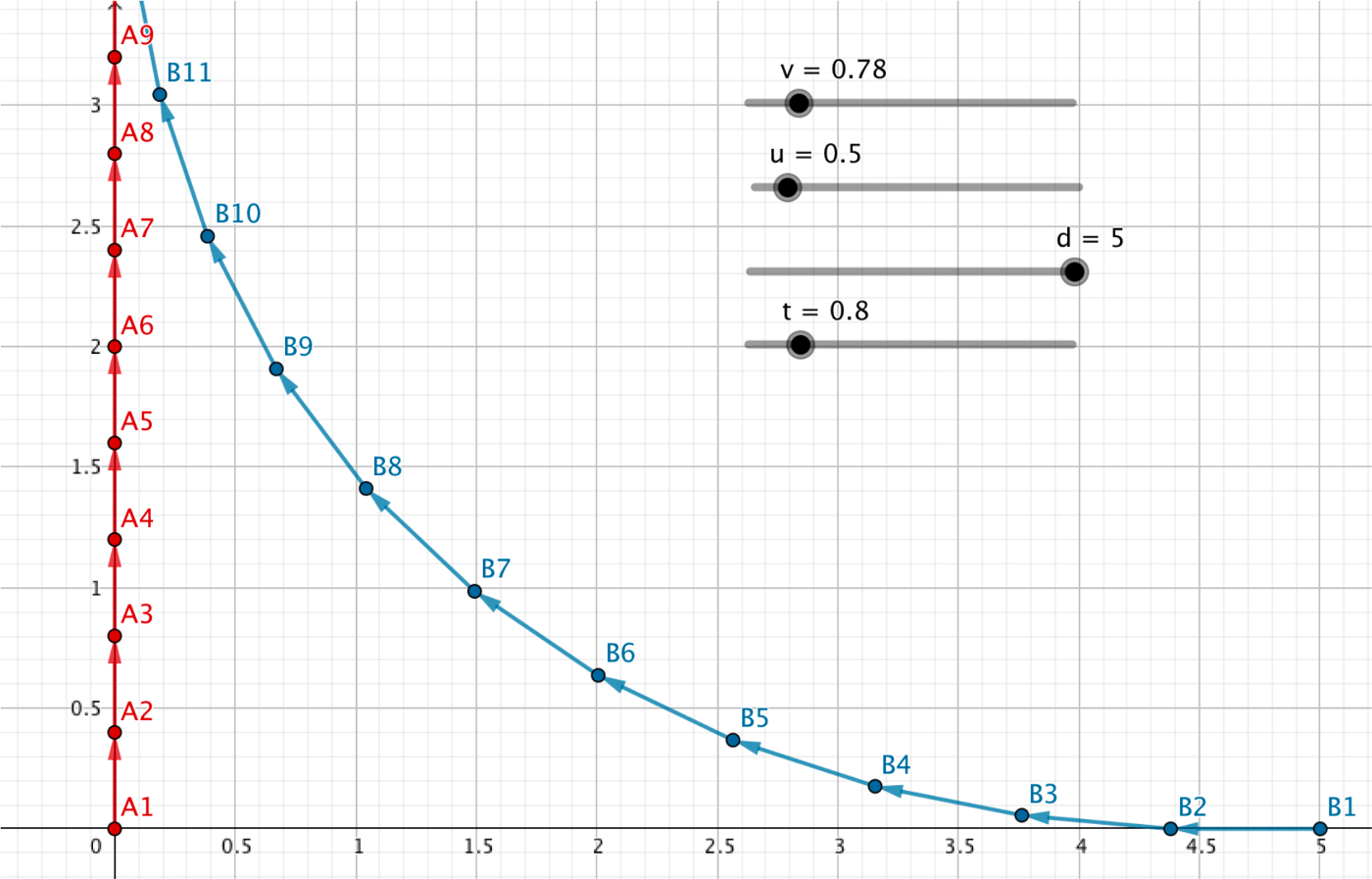
Lägg in fyra glidare.

1. Två glidare \(u\) och \(v\) som representerar haren fart respektive hundens.
2. En glidare \(d\) som representerar det ursprungliga avståndet mellan haren och hunden.
3. En glidare \(t\) som representerar hur lång tid det tar mellan det att hunden tittar upp och tar ut en ny riktning.

Lägg in alla övriga objekt som behövs för modellen.

Du kan behöva använda kommandot Enhetsvektor( <Vektor> ) och kommandot Vektor( <Punkt>, <Punkt> ).

Om modellen förutsätter att hunden aldrig springer ner i floden, dvs aldrig korsar \(y\)-axeln, kan du använda en if-sats, dvs kommandot Om( <Villkor>, <Då>, <Annars> ). Välj själv om hunden ska kunna korsa \(y\)-axeln eller inte.

När du är klar ska du kunna ändra på glidarna för att se olika vägar som hunden och haren tar.